Cho hình chóp SABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = SD GỌI O LÀ tâm của hình thoi và SO =a√3/4 góc ABC bằng 60 độ a. Tính diện tích đáy ABCD b.tính thể tích hình chóp SABCD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đề bài thiếu dữ liệu định vị điểm S (ví dụ SC bằng bao nhiêu đó) nên ko thể tính góc giữa SB và (ABCD)

Có: (SC, (ABCD)) = ∠SCB
Gọi: \(O=AC\cap BD\)
Có: \(OC=\dfrac{1}{2}AC=\dfrac{3}{2}a\)
\(OB=\dfrac{1}{2}BD=\dfrac{5}{2}a\)
Xét tam giác OBC vuông tại O (Do: ABCD là hình thoi nên AC ⊥ BD), có:
\(BC=\sqrt{OB^2+OC^2}=\dfrac{a\sqrt{34}}{2}\)
Xét tam giác SBC vuông tại B (Do: SB ⊥ (ABCD) ), có:
\(SB=BC.tan60^o=\dfrac{a\sqrt{102}}{2}\)
\(\Rightarrow V_{SABCD}=\dfrac{1}{3}.\dfrac{a\sqrt{102}}{2}.\dfrac{1}{2}.3a.5a=\dfrac{5a^3\sqrt{102}}{4}\left(đvtt\right)\)

Đáp án A
Trong mặt phẳng dựng đường thẳng đi qua A và vuông góc vưới SB tại K
Ta chứng minh được
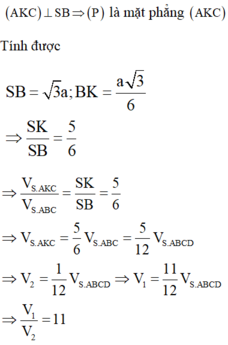

Do O là giao điểm 2 đường chéo \(\Rightarrow\) O là trung điểm AC và BD
Tam giác SAC cân tại S \(\Rightarrow SO\) là trung tuyến đồng thời là đường cao
\(\Rightarrow SO\perp AC\) (1)
Tương tự ta có \(SO\perp BD\) (2)
(1); (2) \(\Rightarrow SO\perp\left(ABCD\right)\)
b. Ta có \(AC\perp BD\) nên tam giác OBC vuông tại O
\(\Rightarrow OE=BE=\dfrac{1}{2}BC\) (trung tuyến ứng với cạnh huyền)
Mà \(\widehat{BCD}=\widehat{BAD}=60^0\Rightarrow\Delta BCD\) đều
\(\Rightarrow BD=BC\Rightarrow OB=BE=\dfrac{1}{2}BC\Rightarrow OB=OE=BE\)
\(\Rightarrow\Delta OBE\) đều \(\Rightarrow OF\perp BC\) (trung tuyến tam giác đều đồng thời là đường cao)
Mà \(SO\perp\left(ABCD\right)\Rightarrow SO\perp BC\)
\(\Rightarrow BC\perp\left(SOF\right)\Rightarrow\left(SBC\right)\perp\left(SOF\right)\)

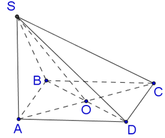

a: Xét ΔBAC có BA=BC và góc ABC=60 độ
nên ΔABC đều
=>\(S_{ABC}=\dfrac{a^2\sqrt{3}}{4}\)
=>\(S_{ABCD}=\dfrac{a^2\sqrt{3}}{2}\)