 câu b ai cứu em với
câu b ai cứu em với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: \(B=\sqrt{\left(2\sqrt{5}-5\right)^2}+\sqrt{29-12\sqrt{5}}\)
\(=\sqrt{\left(5-2\sqrt{5}\right)^2}+\sqrt{\left(2\sqrt{5}-3\right)^2}\)
\(=\left|5-2\sqrt{5}\right|+\left|2\sqrt{5}-3\right|\)
\(=5-2\sqrt{5}+2\sqrt{5}-3=2\)
c: \(C=\dfrac{6}{\sqrt{7}-1}-14\sqrt{\dfrac{1}{7}}+\dfrac{\sqrt{21}+2\sqrt{7}}{2+\sqrt{3}}\)
\(=\dfrac{6\left(\sqrt{7}+1\right)}{7-1}-2\sqrt{7}+\dfrac{\sqrt{7}\left(2+\sqrt{3}\right)}{2+\sqrt{3}}\)
\(=\sqrt{7}+1-2\sqrt{7}+\sqrt{7}=1\)

Lời giải:
4.
$29(19-13)-19(29-13)=29.19-29.13-(19.29-19.13)$
$=29.19-29.13-19.29+19.13=(29.19-19.29)-(29.13-19.13)$
$=0-13(29-19)=0-13.10=-130$
5.
$31(-18)+31(-81)-31=31[(-18)+(-81)-1]=31[-(18+81)-1]=31(-100)=-3100$
6.
$(-12).47+(-12).52+(-12)=(-12)(47+52+1)=(-12).100=-1200$
7.
$13(23+22)-3(17+28)=13.45-3.45=45(13-3)=45.10=450$

5.
\(\Delta=\left(-2\right)^2-4\left(-15\right)=64\)
6.
\(\Delta'=2^2-5.\left(-7\right)=39\)
Mà thầy ơi em hok hiểu khúc đầu làm sao để ra cái đó ròi ra kết quả á :((( cả 2 câu lun

2:
A=(x1-x2)^2-x1^2+x1(x1+x2)
=(x1-x2)^2+x1x2
=(x1+x2)^2-3x1x2
=(1/2)^2-3*(-1/4)=1/4+3/4=1

* yêu cầu :
1, 2 nguyên tố khác loại trở lên
2,chỉ số ở chân mỗi KHHH
3,\(A_xB_y\) - \(A_xB_yC_z\)


2:
a: AD//BC
=>góc AEB=góc EBC
mà góc EBC=góc ABE
nên góc AEB=góc ABE
=>AB=AE
b: Xét ΔEAB và ΔFCD có
góc A=góc C
AB=CD
góc EBA=góc FDC
Do đó: ΔEAB=ΔFCD
=>EA=FC
EA+ED=AD
FC+FB=BC
mà EA=FC và AD=BC
nên ED=FB
Xét tứ giác EDFB có
ED//BF
ED=BF
Do đó: EDFB là hình bình hành

a: Xét ΔAHE có
AM là đường cao
AM là đường trung tuyến
DO đó: ΔAHE cân tại A
hay AH=AE
b: Xét ΔAKI và ΔAHI có
AK=AH
\(\widehat{KAI}=\widehat{HAI}\)
AI chung
Do đó: ΔAKI=ΔAHI
Suy ra: \(\widehat{AKI}=\widehat{AHI}=90^0\)
hay IK//AB
c: Ta có: IK=IH
mà IK<IC
nên IH<IC

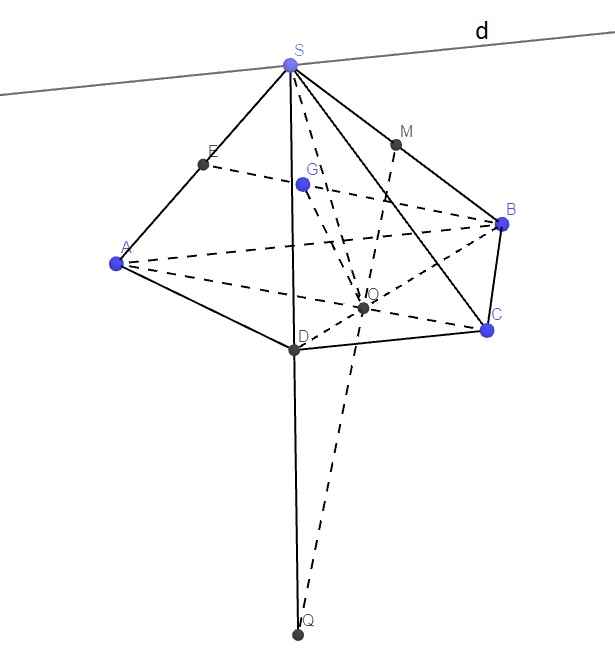
a.
Ta có: \(\left\{{}\begin{matrix}O\in AC\in\left(SAC\right)\\O\in BD\in\left(SBD\right)\end{matrix}\right.\) \(\Rightarrow O=\left(SAC\right)\cap\left(SBD\right)\)
\(S=\left(SAC\right)\cap\left(SBD\right)\)
\(\Rightarrow SO=\left(SAC\right)\cap\left(SBD\right)\)
Do \(AB||CD\Rightarrow\) giao tuyến của (SAC) và (SBD) là một đường thẳng song song AB và CD
Qua S kẻ đường thẳng \(d||AB\)
Do \(S=\left(SAB\right)\cap\left(SCD\right)\Rightarrow d=\left(SAB\right)\cap\left(SCD\right)\)
b.
\(O\in AC\in\left(AMC\right)\Rightarrow OM\in\left(AMC\right)\)
\(\left\{{}\begin{matrix}M\in SB\\O\in BD\end{matrix}\right.\) \(\Rightarrow OM\in\left(SBD\right)\) \(\Rightarrow OM=\left(AMC\right)\cap\left(SBD\right)\)
Trong mp (SBD), kéo dài OM cắt SD tại Q
\(\Rightarrow Q=SD\in\left(AMC\right)\)
c.
Gọi E là trung điểm SA
Do G là trọng tâm tam giác SAB \(\Rightarrow G\in BE\) và \(BG=\dfrac{2}{3}BE\Rightarrow\dfrac{BG}{BE}=\dfrac{2}{3}\) (1)
Do \(AB||CD\) , áp dụng định lý Talet: \(\dfrac{OD}{OB}=\dfrac{CD}{AB}=\dfrac{1}{2}\Rightarrow\dfrac{OD}{OB}+1=\dfrac{3}{2}\Rightarrow\dfrac{OD+OB}{OB}=\dfrac{3}{2}\)
\(\Rightarrow\dfrac{BD}{OB}=\dfrac{3}{2}\Rightarrow\dfrac{BO}{BD}=\dfrac{2}{3}\) (2)
(1);(2) \(\Rightarrow\dfrac{BG}{BE}=\dfrac{BO}{BD}\Rightarrow OG||ED\) (Talet đảo)
Mà \(ED\in\left(SAD\right)\Rightarrow OG||\left(SAD\right)\)
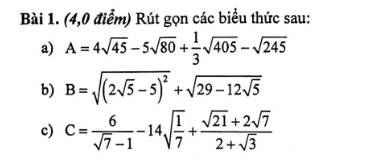
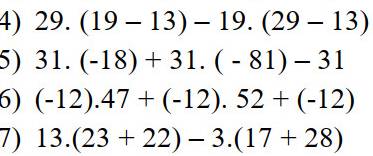





 ai cứu em với ạ em cần nộp trc 7h10 ạ
ai cứu em với ạ em cần nộp trc 7h10 ạ
`b,`
`@` \(\text{Na}_2\text{O}\)
`-` Gồm `2` nguyên tử `Na`, `1` nguyên tử `O`
`@`\(\text{H}_2\text{SO}_4\)
`-` Gồm `2` nguyên tử `H`, `1` nguyên tử `S,` `4` nguyên tử `O`
`@`\(\text{Ca}_3\left(\text{PO}_4\right)_2\)
`-` Gồm `3` nguyên tử `Ca`, `2` nguyên tử `P`, `8` nguyên tử `O`
`@`\(\text{Fe}\left(\text{OH}\right)_3\)
`-` Gồm `1` nguyên tử `Fe`, `3` nguyên `O`, `3` nguyên tử `H`
`@`\(\text{ P}_2\text{O}_5\)
`-` Gồm `2` nguyên tử `P`, `5` nguyên tử `O`.
Cảm ơn bạn rất nhiều