Cho tam giác ABC,đường cao AH,biêt AB=6cm,Ac=8cm.tính AH
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


=1/6^2 + 1/8^2 =25/576
=> AH^2 =576/25
=> AH=24/5
Áp dụng định lí Pytago vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
\(\Leftrightarrow\dfrac{1}{AH^2}=\dfrac{1}{6^2}+\dfrac{1}{8^2}=\dfrac{100}{48^2}\)
\(\Leftrightarrow AH^2=\left(\dfrac{48}{10}\right)^2\)
hay AH=4,8cm
Vậy: AH=4,8cm

a) tam giác ABC vuông tại A nên áp dụng Py-ta-go:
\(\Rightarrow BC^2=AB^2+AC^2=6^2+8^2=100\Rightarrow BC=10\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{6.8}{10}=4.8\left(cm\right)\)
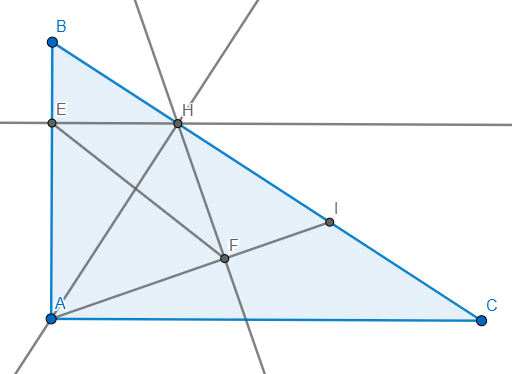
b) tam giác AHB vuông tại H có đường cao HE nên áp dụng hệ thức lượng
\(\Rightarrow AE.AB=AH^2\)
tam giác AHI vuông tại H có đường cao HF nên áp dụng hệ thức lượng
\(\Rightarrow AF.AI=AH^2\Rightarrow AF.AI=AE.AB\Rightarrow\dfrac{AF}{AB}=\dfrac{AE}{AI}\)
Xét \(\Delta AEF\) và \(\Delta AIB:\) Ta có: \(\left\{{}\begin{matrix}\dfrac{AE}{AI}=\dfrac{AF}{AB}\\\angle BAIchung\end{matrix}\right.\)
\(\Rightarrow\Delta AEF\sim\Delta AIB\left(c-g-c\right)\)
1: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8(cm)

góc AEH=góc ADH=góc DAE=90 độ
=>ADHE là hình chữ nhật
góc NED=góc NEH+góc DEH
=góc DAH+góc NHE
=góc BAH+góc B=90 độ
=>NE vuông góc ED(1)
góc MDE=góc MDH+góc EDH
=góc MHD+góc EAH
=góc HAC+góc C=90 độ
=>DM vuông góc ED(2)
Từ (1), (2) suy ra ENMD là hình thang vuông
\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
BH=6^2/10=3,6cm
=>DM=1,8cm
HC=8^2/10=6,4cm
=>EN=3,2cm
AH=6*8/10=4,8cm
=>ED=4,8cm
\(S_{ENMD}=\dfrac{1}{2}\cdot\left(EN+DM\right)\cdot ED=\dfrac{1}{2}\cdot\left(3,2+1,8\right)\cdot2,4=1,2\cdot5=6\left(cm^2\right)\)

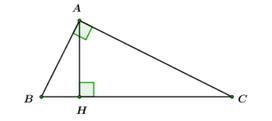
+) Chứng minh tam giác ABC vuông
Ta có:
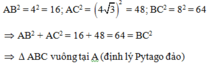
+) Tính số đo B, C và độ dài đường cao AH của ABC
Áp dụng tỉ số lượng giác của góc nhọn trong ABC và có đường cao AH ta có:
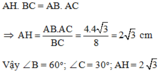
Đáp án cần chọn là: D


tam giác ABC có vuông ko?
tam giác ABC là tam giác vuông hả bn?