Một ca nô xuôi dòng từ A đến B mất 2 giờ và ngược dòng từ B về A mất 2 giờ 30 phút. Tính khoẳng cách giữa A và B, biết rằng vận tốc của dòng nước là 2km
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi vân tốc của ca nô là x(km/h)(x>0)
vậy quãng đường đi từ A đến B là 2x
Vậy vân tốc đi ngược dòng là x-3
2 giờ 30 phút = 2,5 h
=> Quãng đường đi từ B đến A là 2,5(x-3)
Từ đó ta có phương trình:
2x = 2,5(x-3)
<=> 2x = 2,5x - 7,5 <=> 0,5x = 7,5
<=> x = 15 (TMĐK)
=> Khoảng cách từ A đến B là 2.15= 30km

Gọi vận tốc của thuyền là v ta có:
Khi xuôi dòng : \(v+2\)
Khi ngược dòng: \(v-2\)
Do quãng đường không đổi nên ta có phương trình:
\(6.\left(v+2\right)=7.\left(v-2\right)\Leftrightarrow6v+12=7v-14\Leftrightarrow v=26\)(km/h)
\(\Rightarrow S=v_{ngược}\times t_{ngược}=\left(v-v_{nước}\right)\times t_{ngược}=\left(26-2\right)\times7=168\left(km\right)\)
Vậy quãng đường AB dài 168 km

Gọi quãng đường AB là : x (x > 0)
Vận tốc lượt đi là : \(\frac{x}{6}\)
Vận tốc lượt về là : \(\frac{x}{7}\)
Vận tốc đi lớn hơ nvaanj tốc về là : 2 x 2 = 4 (km/h)
Ta có : \(\frac{x}{6}-\frac{x}{7}=4\)
\(\Leftrightarrow7x-6x=168\)
\(\Leftrightarrow x=168\)
Vây quãng AB dài 168 km

Gọi x là khoảng cách từ A đến B
ta có : Hiệu vận tốc xuôi dòng và ngược dòng gấp 2 lần vận tốc dòng nước, hay ta có :
\(\frac{x}{4}-\frac{x}{5}=2\times2\) hay \(\frac{x}{20}=4\Leftrightarrow x=80km\)

Gọi x (km) là khoảng cách giữa hai bến A và B, với x > 0.
Vì vận tốc xuôi dòng lớn hơn vận tốc ngược dòng chính bằng 2 lần vận tốc dòng nước nên ta có phương trình:
x = 80 (thỏa mãn điều kiện).
Vậy khoảng cách giữa hai bến A và B là 80km.
(Giải thích tại sao hiệu vận tốc xuôi dòng và ngược dòng bằng 2 lần vận tốc dòng nước:
Nếu gọi vận tốc canô là v (km/h), vận tốc dòng nước là a (km/h), ta có:
Khi xuôi dòng: vận tốc canô = v + a
Khi ngược dòng: vận tốc canô = v - a
Hiệu vận tốc = v + a - (v - a) = 2a = 2 vận tốc dòng nước.)
Gọi vận tốc thực cano là x ( km/h, > 0 )
Vận tốc ngược dòng : x - 2 km/h
Vận tốc xuôi dòng : x + 2 km/h
Quãng đường từ AB khi đi ngược dòng : 5( x - 2 ) km
Quãng đường từ AB khi đi xuôi dòng : 4( x + 2 ) km
Vì quãng đường ko đổi nên ta có phương trình
\(5\left(x-2\right)=4\left(x+2\right)\Leftrightarrow5x-10=4x+8\Leftrightarrow x=18\)km/h
Quãng đường AB dài : \(4\left(18+2\right)=4.20=80\)km

Gọi z là quãng đường khoảng cách giữa A và B (x>0)
Khi đó vận tốc lượt đi \(\dfrac{x}{\dfrac{1}{2}}\left(km/\right)h\)
Và vận tốc lượt về: \(\dfrac{x}{\dfrac{3}{5}}\left(km/h\right)\)
Vận tốc lúc đi lớn hơn vận tốc lúc về là: \(2.2=4\left(km/h\right)\)
Vậy ta có phương trình:
\(\dfrac{x}{\dfrac{1}{2}}-\dfrac{x}{\dfrac{3}{5}}=4\)
\(\Leftrightarrow\dfrac{\dfrac{3}{5}x}{\dfrac{3}{10}}-\dfrac{\dfrac{1}{2}x}{\dfrac{3}{10}}=\dfrac{\dfrac{6}{5}}{\dfrac{3}{10}}\)
\(\Leftrightarrow\dfrac{3}{5}x-\dfrac{1}{2}x=\dfrac{6}{5}\)
\(\Leftrightarrow\dfrac{1}{10}x=\dfrac{6}{5}\)
\(\Leftrightarrow x=\dfrac{\dfrac{6}{5}}{\dfrac{1}{10}}=12\left(km\right)\left(tmđk\right)\)
Vậy quãng đường AB dài 12 km

Gọi x (km) là khoảng cách giữa hai bến A và B, với x > 0.
x = 80 thỏa mãn điều kiện.
Vậy khoảng cách giữa hai bến A và B là 80km.
(Giải thích tại sao hiệu vận tốc xuôi dòng và ngược dòng bằng 2 lần vận tốc dòng nước:
Nếu gọi vận tốc canô là v (km/h), vận tốc dòng nước là a (km/h), ta có:
Khi xuôi dòng: vận tốc canô = v + a
Khi ngược dòng: vận tốc canô = v - a
Hiệu vận tốc = v + a - (v - a) = 2a = 2 vận tốc dòng nước.)
gọi vận tốc ca nô là x(km) ĐK:x>0
Vận tốc ca nô xuôi dòng từ A đến B là x+2(km/h)
Vận tốc ca nô ngược dòng từ B đến A là x-2(km/h)
Quãng đường ca nô đi xuôi dòng từ A đến B là 4(x+2) (km)
Quãng đường ca nô đi ngược dòng từ B đến A là 5(x-2) (km)
Theo đề, ta có phương trình:
4(x+2)=5(x-2)
<=> 4x+8=5x-10
<=>x=18(thỏa mãn điều kiện)
Vậy khoảng cách giữa A và B là 4(18+2)=80km

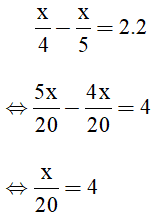


Gọi vận tốc thật là x
Theo đề, ta có: 2(x+2)=2,5(x-2)
=>2x+4=2,5x-5
=>-0,5x=-9
=>x=18
=>AB=2(18+2)=40km