Cho 2 đường tròn $\left(O_1\right)$ và $\left(O_2\right)$cắt nhau tại A và B, tiếp tuyến chung với 2 đường tròn $\left(O_1\right)$và $\left(O_2\right)$về phía nửa mặt phẳng bờ \(O

OI

o0o I am a studious person o0o

6 tháng 5 2017 - olm

Cho 2 đường tròn $\left(O_1\right)$ và $\left(O_2\right)$cắt nhau tại A và B, tiếp tuyến chung với 2 đường tròn $\left(O_1\right)$và $\left(O_2\right)$về phía nửa mặt phẳng bờ $O_1;O_2$ chưa điểm B, có tiếp điểm thứ tự là E , F. Qua A kẻ cát tuyến song song với EF và cắt $\left(O_1\right),\left(O_2\right)$theo thứ tự tại C và D. Đường thẳng CE và đường thẳng DF cắt nhau tại I . CMR : a ) IA vuông góc...

Đọc tiếp

#Toán lớp 9

1

LV

Lầy Văn Lội

6 tháng 5 2017

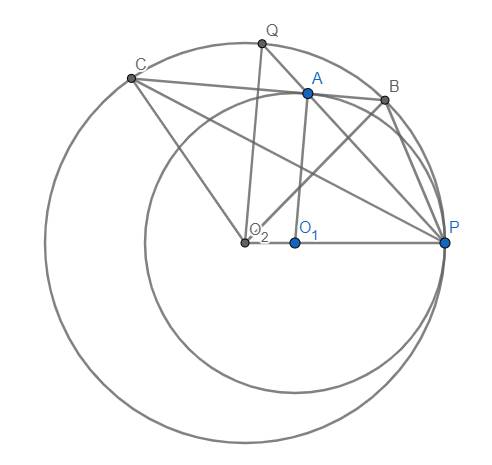
a) kéo dài O₁E,O₂F cắt CD ở M và N

b) góc BFI + góc BEI =180

c) gọi AB cắt EF ở K

bằng đồng dạng ta chứng minh được KE=KF=KB.KA(đpcm)

Đúng(0)

KN

Khiêm Nguyễn Gia

2 tháng 1 - olm

Cho các đường tròn $\left(O_1;R_1\right)$ và $\left(O_2;R_2\right)$ tiếp xúc trong tại $P$ $\left(R_2R_1\right)$. Tiếp tuyến tại $A$ của đường tròn $\left(O_1\right)$ cắt $\left(O_2\right)$ tại $B$ và $C$. Chứng minh rằng: $PA$ là tia phân giác...

Đọc tiếp

#Toán lớp 9

1

LS

Lê Song Phương

2 tháng 1

Gọi Q là giao điểm của PA và (O₂). Do $\widehat{O_1AP}=\widehat{O_1PA}=\widehat{O_2PQ}=\widehat{O_2QP}$ nên O₁A//O₂Q

Mặt khác, $BC\perp O_1A$ (vì BC là tiếp tuyến tại A của (O₁) nên $BC\perp O_2Q$

$\Rightarrow$ Q là điểm chính giữa của cung nhỏ BC

$\Rightarrow$ PQ là tia phân giác $\widehat{BPC}$ $\Rightarrow$ đpcm

Đúng(1)

KN

Khiêm Nguyễn Gia

2 tháng 1

Cho các đường tròn $\left(O_1;R_1\right)$ và $\left(O_2;R_2\right)$ tiếp xúc trong tại $P$ $\left(R_2R_1\right)$. Tiếp tuyến tại $A$ của đường tròn $\left(O_1\right)$ cắt $\left(O_2\right)$ tại $B$ và $C$. Chứng minh rằng: $PA$ là tia phân giác của...

Đọc tiếp

#Toán lớp 9

0

CH

Cô Hoàng Huyền

Admin VIP

22 tháng 3 2021 - olm

Cho nửa đường tròn $(O)$ đường kính $AB$. $M$ là điểm tùy ý trên nửa đường tròn ($M$ khác $A$ và $B$). Kẻ $MH\perp AB$ $\left(H\in AB\right)$. Trên cùng nửa mặt phẳng bờ $AB$ chứa nửa đường tròn $(O)$, vẽ hai nửa đường tròn tâm $O_1$ đường kính $AH$ và tâm $O_2$ đường kính $BH$. $MA$ và $MB$ cắt hai nửa đường tròn $\left(O_1\right)$ và $\left(O_2\right)$ lần lượt tại $P$ và $Q$. a) Chứng minh...

Đọc tiếp

#Toán lớp 9

22

H

Hậu

1 tháng 2 2022

Đúng(0)

NN

Ngô Nhật Hạ

21 tháng 2 2022

a) Vì AH, HB, AB đều là các đường kính của các nửa đường tròn (O₁) , (O₂) và (O) nên tứ giác MPHQ có ba góc P, Q, M vuông. Vì vậy nó là hình chữ nhật.

Từ đó, ta có HM = PQ.
b) Vì MHPQ là hình chữ nhật nên $\widehat{MPQ}=\widehat{MHQ}=\widehat{MBH}\left(=\dfrac{\stackrel\frown{HQ}}{2}\right)$ , do đó APQB là tứ giác nội tiếp.

c) Ta có $\widehat{O_1PA}=\widehat{PAO_1}=90^o-\widehat{HMP}=90^o-\widehat{MPQ}$

$\Rightarrow\widehat{O_1PA}+\widehat{MPQ}=90^o\Rightarrow\widehat{O_1PQ}=90^o$ nên PQ tiếp xúc nửa đường tròn (O₁) tại P.

Tương tự , PQ tiếp xúc (O₂) tại Q hay PQ là tiếp tuyến chung của hai nửa đường tròn (O₁) và (O₂)

Đúng(0)

HH

hh hh

25 tháng 1 2017 - olm

cho AB=18 cm. C$\in$AB: AC=6 cmtrên cùng một nửa mặt phẳng bờ AB vẽ nửa đường tròn $\left(O_1;\frac{AC}{2}\right)$và nửa đường tròn $\left(O_2;\frac{BC}{2}\right)$. Vẽ tiếp tuyến chung ngoài MK ($\left(M\in\left(O_1\right)\right)$;$\left(K\in\left(O_2\right)\right)$ ) AM cắt BK ở I; MK cắt đường tròn $\left(O;\frac{AB}{2}\right)$ở E;D. Chứng minh:a)$CI⊥AB$b)Tính...

Đọc tiếp

#Toán lớp 9

0

KV

Khương Vũ Phương Anh

17 tháng 9 2017 - olm

Cho 2 dường tròn (O₁,5cm) và (O₂,2cm) nằm ngoài nhau. 1 tiếp tuyền chung ngoài AB của 2 đường tròn, $A\in(O_1),B\in\left(O_2\right)$ và 1 tiếp tuyến chung trong CD của 2 đường tròn, $C\in\left(O_1\right),D\in\left(O_2\right)$. Tính độ dài đoạn nối tâm O₁O₂ biết AB=1,5 CD

#Toán lớp 9

1

CH

Cô Hoàng Huyền

Admin VIP

18 tháng 9 2017

Gọi giao điểm của O₁O₂ và CD là I.

Ta thấy rằng $\Delta O_1CI\sim\Delta O_2DI$ theo tỉ số đồng dạng là $k=\frac{O_1C}{O_2D}=\frac{5}{2}$

Đặt $ID=2x\left(cm\right)\Rightarrow IC=5x\Rightarrow CD=7x\Rightarrow AB=1,5.7x=10,5x$

Theo Pitago ta cũng có $O_1I=\sqrt{25x^2+25};O_2I=\sqrt{4x^2+4}\left(1\right)$

Xét hình thang vuông ABO₂O₁ , kẻ O₂H vuông góc với AO₁ , ta tính được $HO_1=5-2=3\left(cm\right)$

Vậy thì $O_1O_2^2=O_2H^2+HO_1^2\Rightarrow O_1O_2=\sqrt{110,25x^2+9}\left(2\right)$

Từ (1) và (2) suy ra $\sqrt{110,25x^2+9}=\sqrt{25x^2+25}+\sqrt{4x^2+4}$

$\Leftrightarrow\sqrt{110,25x^2+9}=5\sqrt{x^2+1}+2\sqrt{x^2+1}$

$\Leftrightarrow\sqrt{110,25x^2+9}=7\sqrt{x^2+1}$

$\Leftrightarrow110,25x^2+9=49x^2+49$

$\Leftrightarrow x^2=\frac{32}{49}\Rightarrow O_1O_2=7.\sqrt{\frac{32}{49}+1}=9\left(cm\right)$

Vậy O₁O₂ = 9 cm.

Đúng(0)

CG

Cô gái thất thường (Ánh Dương)

6 tháng 9 2019 - olm

Cho hai đường tròn $\left(O_1\right),\left(O_2\right)$cắt nhau tại A và B, kéo dài AB về phía B lấy điểm M, từ M kẻ tiếp tuyến ME và MF với $\left(O_1\right)$( E và F là hai tiếp điểm, F cùng phía với đường tròn $\left(O_2\right)$đối với AB. ĐƯờng thẳng BE và BF cắt $\left(O_2\right)$ tại P, Q. PQ và EF cắt nhau tại I. CMR:a) $\frac{FB}{FA}=\frac{EB}{EA}$ b) AFIQ là tứ giác nội...

Đọc tiếp

#Toán lớp 9

0

CH

Cô Hoàng Huyền

Admin VIP

20 tháng 3 2021 - olm

Cho hai đường tròn tâm $O_1,O_2$ tiếp xúc ngoài nhau tại $A$. Trên đường tròn $\left(O_1\right)$ lấy hai điểm $B$, $C$ phân biệt khác $A$. Các đường thẳng $BA$, $CA$ cắt đường tròn $\left(O_2\right)$ tại $P$ và $Q$. Chứng minh $PQ$//$BC$.

#Toán lớp 9

9

TX

Trần Xuân Tài

15 tháng 12 2021

ta có : Góc CAB = GÓc PQG ( 2 góc đối đỉnh ) . theo tính chất của góc nt , taco : Góc CBA = 1/2 cung AC . Góc APQ = 1/2 sd AQ(1) . theo t/c của góc tạo bởi tia tiếp tuyến và dây cung ta có ; GÓC CBA = 1/2 cung AC . APQ + 1/2 sđ AQ ( 2) . TỪ (1) , ( 2 ) => GÓC CBA = APQ . mà 2 góc này ở vị trí soletrong = > BC song song với QP

Đúng(0)

NT

Nguyễn Trọng Trung

15 tháng 12 2021

xAC=QAy(hai góc đối đỉnh)

theo tính chất của 2 góc được tạo bởi tia tiếp tuyến

=> xAC=1/2sđ cung AC,QAy=1/2sđ cungAQ(1)

theo tính chất của góc nội tiếp,ta có

=> ABC=1/2 sđ cung AC,APQ=1/2sđ cung AQ(2)

từ (1),(2)=> ABC=APQ

=> QP//BC

Đúng(0)

HP

Hoàng Phúc

4 tháng 11 2016 - olm

Cho 2 đường tròn $\left(O_1;R_1\right)$ và $\left(O_2;R_2\right)$ tiếp xúc ngoài với nhau tại A,với $R_1=3;R_2=5$ .Tiếp tuyến chung ngoài tiếp xúc 2 đường tròn lần lượt tại B,C.Tính phần diện tích tam giác ABC nằm ngoài cả 2 hình tròn đã cho

#Toán lớp 9

2

HL

Hoàng Lê Bảo Ngọc

5 tháng 11 2016

Từ O₁ kẻ O₁H vuông góc với O₂C tại H. Vì R₂ > R₁ nên ta được O₁BCH là hình chữ nhật

và : O₂H = R₂ - R₁ = 2

$cos\widehat{O_1O_2H}=\frac{O_2H}{O_1O_2}=\frac{2}{8}=\frac{1}{4}\Rightarrow\widehat{O_1O_2H}=\alpha$(Bạn bấm máy tính để tìm giá trị góc này, còn mình đặt là $\alpha$cho dễ nhìn)

$\Rightarrow\widehat{BO_1O_2}=180^o-\alpha$(BO₁ // CO₂)

$AB=\sqrt{2R^2_1-2R_1^2.cos\left(180^o-\alpha\right)}=m$

$AC=\sqrt{2R_2^2-2R_2^2.cos\alpha}=n$

Gọi $S_1$ và $S_2$ lần lượt là diện tích hình quạt $O_1AB$ và $O_2AC$ thì ta có :

$S_1=\frac{\pi.R_1^2.\left(180^o-\alpha\right)}{360^o}$ ; $S_2=\frac{\pi.R_2^2.\alpha}{360^o}$

$S_{\Delta O_1AB}=\frac{1}{2}.R_1^2.sin\left(90^o-\alpha\right)$; $S_{\Delta O_2AC}=\frac{1}{2}R_2^2.sin\alpha$

Diện tích hình viên phân giới hạn bởi AB là : $S'=S_1-S_{\Delta O_1AB}=x$

Diện tích hình viên phân giới hạn bởi AC là : $S''=S_2-S_{\Delta O_2AC}=y$

Diện tích tam giác ABC nằm ngoài cả hai đường tròn đã cho là :

$S_{ABC}-S'-S''=\frac{1}{2}m.n-x-y$

Đúng(0)

HL

Hoàng Lê Bảo Ngọc

5 tháng 11 2016

HÌNH VẼ ĐÂY :

Đúng(0)

CH

Cô Hoàng Huyền

Admin VIP

20 tháng 3 2021 - olm

Cho ba đường tròn $\left(O_1\right),\left(O_2\right),\left(O_3\right)$ có cùng bán kính $r$ và tiếp xúc ngoài nhau từng đôi một tại $A$, $B$, $C$. Tính diện tích tam giác có ba đỉnh là tiếp điểm.

#Toán lớp 9

56