Lớp 7A có 20 bạn nam và 20 bạn nữ. Giáo viên gọi ngẫu nhiên 1 bạn lên bảng để kiểm tra bài tập. Xác suất để cô gọi được bạn nữ là:
A. \(\dfrac{1}{6}\) B. 1 C .\(\dfrac{1}{3}\) D. \(\dfrac{1}{2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
a) Hai biến cố A và B đồng khả năng vì đều có 5 khả năng cô gọi trúng bạn nam và 5 khả năng cô gọi trúng bạn nữ
b) Vì có 2 biến cố đồng khả năng và luôn xảy ra 1 trong 2 biến cố A và B nên xác suất của mỗi biến cố đó là \(\dfrac{1}{2}\)
HQ
Hà Quang Minh
Giáo viên
1 tháng 10 2023
Cách chọn 2 bạn từ 7 bạn là \(C_{7}^2 \Rightarrow n\left( \Omega \right) = C_{7}^2 = 21\)
Gọi A là biến cố: “Hai bạn được chọn có một bạn nam và một bạn nữ”.
Cách chọn một bạn nam là: 3 cách chọn
Cách chọn một bạn nữ là: 4 cách chọn
Theo quy tắc nhân ta có \(n\left( A \right) = 3.4 = 12\)
Vậy xác suất của biến cố A là \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{12}}{{21}} = \frac{4}{7}\).
Chọn A
CM
10 tháng 1 2019
Không gian mẫu là số cách gọi ngẫu nhiên 2 nam, 2 nữ từ 46 học sinh.
Suy ra số phần tử của không gian mẫu là 
.
Gọi A là biến cố 4 học sinh (2 nam, 2 nữ) được gọi lên đều không chuẩn bị bài tập về nhà, trong đó có Bình và Mai . Ta mô tả khả năng thuận lợi cho biến cố A như sau:
● Gọi Bình và Mai lên bảng, có 1 cách.
● Tiếp theo gọi 1 bạn nam từ 6 bạn không làm bài tập về nhà còn lại và 1 bạn nữ từ 3 bạn không làm bài tập về nhà còn lại, có 
cách.
Suy ra số phần tử của biến cố A là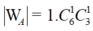 
.
Vậy xác suất cần tính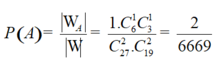 
.
Chon C.
CM
3 tháng 1 2017
Đáp án B
Có các trường hợp sau:
+ 1 nam, 3 nữ, suy ra có C 18 1 C 17 3 cách gọi
+ 2 nam, 2 nữ, suy ra có C 18 2 C 17 2 cách gọi
+ 3 nam, 1 nữ, suy ra có C 18 3 C 17 1 cách gọi
Suy ra xác suất sẽ bằng
CM
24 tháng 5 2019
Đáp án B
Có các trường hợp sau:
+ 1 nam, 3 nữ, suy ra có C 18 1 C 17 3 cách gọi
+ 2 nam, 2 nữ, suy ra có C 18 2 C 17 2 cách gọi
+ 3 nam, 1 nữ, suy ra có C 18 3 C 17 1 cách gọi
Suy ra xác suất sẽ bằng
CM
30 tháng 12 2019
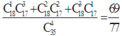
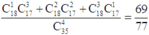
Đáp án B
Phương pháp: Xác suất : P ( A ) = n ( A ) n ( Ω )
Cách giải:
Số phần tử của không gian mẫu : n ( Ω ) = C 15 + 10 4 = C 25 4
Gọi A là biến cố : “4 học sinh được gọi đó cả nam lẫn nữ”
Khi đó :
Xác suất cần tìm:
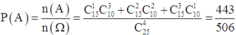
Chọn ngẫu nhiên có 40 cách chọn
Chọn 1 bạn nữa lên bảng có 20 cách chọn
=> Xác xuất \(\dfrac{20}{40}=\dfrac{1}{2}=>D\)