Cho nữa đường tròn (O), đường kính AB. Gọi C và D là hai điểm trên nữa đường tròn ( C thuộc cung AD) , AD và BD cắt nhau ở E, AD và BC cắt nhau ở F. Chứng minh: a. Tứ giác ECFD nội tiếp được một đường tròn. b Góc AEF= góc ADC C. Cho góc AOC =50° và OC= 3cm, tính diện tích hình quạt tròn AOC. Giúp mình gấp với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
14 tháng 7 2023
Lời giải:
a.
Ta thấy $\widehat{ACB}=\widehat{ADB}=90^0$ (góc nội tiếp chắn nửa đường tròn)
$\Rightarrow \widehat{ECF}=180^0-\widehat{ACB}=180^0-90^0=90^0$; $\widehat{EDF}=180^0-\widehat{ADB}=180^0-90^0=90^0$
Tứ giác $ECFD$ có tổng 2 góc đối $\widehat{ECF}+\widehat{EDF}=90^0+90^0=180^0$ nên $ECFD$ là tứ giác nội tiếp.
b.
Vì $ECFD$ là tứ giác nội tiếp nên $\widehat{AEF}=\widehat{CEF}=\widehat{CDF}=\widehat{ADC}$ (góc nt chắn cung $CF$)
CM
20 tháng 10 2017
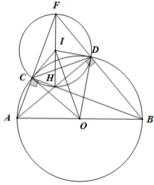
a) Vì C, D thuộc nửa đường tròn đường kính AB nên
A C B = A D B = 90 o ⇒ F C H = F D H = 90 o ⇒ F C H + F D H = 180 o
Suy ra tứ giác CHDF nội tiếp
b) Vì AH ⊥ BF, BH ⊥ AF nên H là trực tâm ∆ AFB ⇒ FH ⊥ AB
⇒ C F H = C B A ( = 90 o − C A B ) ⇒ Δ C F H ~ Δ C B A ( g . g ) ⇒ C F C B = C H C A ⇒ C F . C A = C H . C B
12 tháng 5 2023
a: góc ANM+góc ACM=180 độ
=>ANMC nội tiếp
b: Xét ΔANM vuông tại N và ΔADB vuông tại D có
góc NAM chung
=>ΔANM đồng dạng với ΔADB
=>AN/AD=AM/AB
=>AM*AD=AN*AB
13 tháng 3 2023
a: góc ACB=1/2*180=90 độ
=>góc FCE=90 độ
góc ADB=1/2*180=90 độ
=>gó FDE=90 độ
Vì góc FCE+góc FDE=180 độ
nên FCED nội tiếp
b: Đề sai rồi bạn vì F,C,A thẳng hàng
c: góc ICO=góc ICE+góc OCE
=góc IEC+góc OBE
=90 độ-góc CBA+góc CBA
=90 độ
=>CI là tiếp tuyến của (O)
13 tháng 3 2023
a: góc ACB=1/2*180=90 độ
=>góc FCE=90 độ
góc ADB=1/2*180=90 độ
=>gó FDE=90 độ
Vì góc FCE+góc FDE=180 độ
nên FCED nội tiếp
b: Đề sai rồi bạn vì F,C,A thẳng hàng
c: góc ICO=góc ICE+góc OCE
=góc IEC+góc OBE
=90 độ-góc CBA+góc CBA
=90 độ
=>CI là tiếp tuyến của (O)
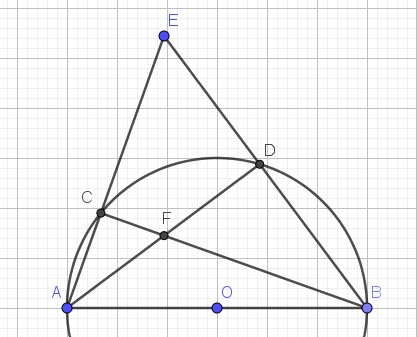
a: góc ACB=góc ADB=90 độ
=>ACDB nội tiếp và BC vuông góc AE, AD vuông góc BE
góc ECF+góc EDF=180 độ
=>ECFD nội tiếp
b: ECFD nội tiếp
=>góc CEF=góc CDF
=>góc AEF=góc ADC
c: \(S_{q\left(AOC\right)}=\dfrac{pi\cdot3^2\cdot50}{360}=\dfrac{pi\cdot5}{4}\)