1, cho bảng tần số
| Thì gian(x) | 6 | 7 | 8 | 9 | 10 |
| tần số (n) | 3 | 5 | 23 | n | 2 |
Tìm giá trị n biết số trung bình cộng là 8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có số trung bình cộng của các giá trị trong bảng là:
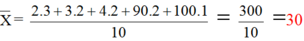
Trong trường hợp này không nên dùng số trung bình cộng làm đại diện cho dấu hiệu vì các giá trị của dấu hiệu chênh lệch đối với nhau quá lớn.

Ta có: X=\(\dfrac{\left(5.2\right)+\left(6.x\right)+\left(7.6\right)+\left(8.4\right)+\left(1.1\right)}{2+x+6+4+1}\)= 7,0
X=\(\dfrac{10+\left(6.x\right)+42+32+1}{x+13}\)= 7,0
⇒ \(\dfrac{6.x+85}{x+13}\)= 7,0
⇒ 7,0.(\(x.13\))=\(6.x+85\)
⇒ 7,0\(x+\) 7,0.13 = \(6x+85\)
⇒ 7,0\(x\) + 91= \(6x+85\)
⇒ 7,0\(x-6x\) = 91- 85
⇒ 1\(x\) = 6
⇒ \(x=\dfrac{6}{1}=6\)
Vậy giá trị \(x\) cần tìm là 6

Trung bình cộng là 4,8
=>\(\dfrac{2\cdot6+3\cdot4+9\cdot n+3\cdot10}{6+4+n+3}=4,8\)
=>\(\dfrac{9n+54}{n+13}=4,8\)
=>9n+54=4,8n+62,4
=>4,2n=8,4
=>n=2

Lời giải:Giá trị trung bình cộng là:
\(\frac{5.3+6.4+7.c+8.4+9.d+10.2}{3+4+c+4+d+2}=7,5\)
\(\Leftrightarrow \frac{91+7c+9d}{13+c+d}=7,5\) \(\Leftrightarrow \frac{91+7c+9d}{13+9}=7,5\Rightarrow 7c+9d=74\) (1)
Vì $c+d=9\Rightarrow c=9-d$. Thay vào $(1)$ ta có:
$7(9-d)+9d=74$
$\Rightarrow d=5,5$
$c=9-5,5=3,5$
Nghe sai sai, bạn xem lại đề.

Theo đề ta có: TBC=5,65
\(\Rightarrow\)2.3+3.4+4.5+5.8+6.7+7.2+m.9+10.2 / 40 = 5,65
\(\Rightarrow\)154+9m=5,65.40
\(\Rightarrow\)154+9m=226
\(\Rightarrow\)9m=226-154
\(\Rightarrow\)9m=72
\(\Rightarrow\)m=72/9=8
Vậy giá trị của m là 8
Thiếu số giá trị bạn ơi
@Đào Trọng Chân Làm gì thiếu cái gì hả bạn? Đầy đủ hết rồi mà?
Ta có : X = ( 6 .3 ) + ( 7 . 5 ) + ( 8 . 23 ) + ( 9 . n ) + ( 10 . 2 ) / 3 + 5 + 23 + n + 2 = 8
<=> X = ( 6 .3 ) + ( 7 . 5 ) + ( 8 . 23 ) + ( 9 . n ) + ( 10 . 2 ) / 33 + n = 8
<=> X = 257 + 9 . n / 33 + n = 8
<=> X = 257 + 9 . n = 8 . ( 33 + n )
<=> X = 257 + 9 . n = 264 + 8n
<=> X = 9n - 8n = 264 - 257
<=> X = n = 7
Vậy n = 7
Bài này đúng rồi nhé, nhớ k cho mình nha .