Xác định giá trị của m để bất đẳng thức 3mx>x+2 thỏa mãn với mọi giá trị của x>1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x^2-x+1-m=0\)
Theo Vi - ét, ta có :
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=1\\x_1x_2=\dfrac{c}{a}=1-m\end{matrix}\right.\)
Ta có :
\(5\left(\dfrac{1}{x_1}+\dfrac{1}{x_2}\right)-x_1x_2+4=0\)
\(\Leftrightarrow5\left(\dfrac{x_2+x_1}{x_1x_2}\right)-x_1x_2+4=0\)
\(\Leftrightarrow5\left(\dfrac{1}{1-m}\right)-\left(1-m\right)+4=0\)
\(\Leftrightarrow\dfrac{5}{1-m}-1+m+4=0\)
\(\Leftrightarrow\dfrac{5}{1-m}+m+3=0\)
\(\Leftrightarrow\dfrac{5+m\left(1-m\right)+3\left(1-m\right)}{1-m}=0\)
\(\Leftrightarrow5+m-m^2+3-3m=0\)
\(\Leftrightarrow-m^2-2m+8=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=2\\m=-4\end{matrix}\right.\)

a: Trường hợp 1: m=0
Bất phương trình sẽ là \(0x^2+3\cdot0\cdot x+0+1>0\)
=>1>0(luôn đúng)
Trường hợp 2: m<>0
\(\text{Δ}=\left(3m\right)^2-4m\left(m+1\right)\)
\(=9m^2-4m^2-4m=5m^2-4m\)
Để phương trình có nghiệm đúng với mọi số thực x thì \(\left\{{}\begin{matrix}m\left(5m-4\right)< 0\\m>0\end{matrix}\right.\Leftrightarrow0< m< \dfrac{4}{5}\)
Vậy: 0<=m<4/5
b: Trường hợp 1: m=4
\(g\left(x\right)=\left(4-4\right)\cdot x^2+\left(2\cdot4-8\right)x+4-5=-1< 0\)(luôn đúng)
Trường hợp 2: m<>4
\(\text{Δ}=\left(2m-8\right)^2-4\left(m-4\right)\left(m-5\right)\)
\(=4m^2-32m+64-4\left(m^2-9m+20\right)\)
\(=4m^2-32m+64-4m^2+36m-80\)
=4m-16
Để bất phương trình luôn âm thì \(\left\{{}\begin{matrix}4m-16< 0\\m-4< 0\end{matrix}\right.\Leftrightarrow m< 4\)
Vậy: m<=4

\(x^2-x+1-m=0\left(1\right)\\ \text{PT có 2 nghiệm }x_1,x_2\\ \Leftrightarrow\Delta=1-4\left(1-m\right)\ge0\\ \Leftrightarrow4m-3\ge0\Leftrightarrow m\ge\dfrac{3}{4}\\ \text{Vi-ét: }\left\{{}\begin{matrix}x_1+x_2=1\\x_1x_2=1-m\end{matrix}\right.\\ \text{Ta có }5\left(\dfrac{1}{x_1}+\dfrac{1}{x_2}\right)-x_1x_2+4=0\\ \Leftrightarrow5\cdot\dfrac{x_1+x_2}{x_1x_2}-x_1x_2+4=0\\ \Leftrightarrow\dfrac{5}{1-m}+m-1+4=0\\ \Leftrightarrow\dfrac{5}{1-m}+m+3=0\\ \Leftrightarrow5+\left(1-m\right)\left(m+3\right)=0\\ \Leftrightarrow m^2+2m-8=0\\ \Leftrightarrow m^2-2m+4m-8=0\\ \Leftrightarrow\left(m-2\right)\left(m+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=2\left(n\right)\\m=-4\left(l\right)\end{matrix}\right.\)
Vậy $m=2$

(ax+b)(x2+cx+1)=x3-3x+2
ax3+acx2+ax+bx2+cbx+b=x3-3x+2
ax3+(acx2+bx2)+(ax+cbx)+b=X3-3x+2
ax3+x2(ac+b)+x(a+cb)+b=x3+0x2-3x+2
Đồng nhất các hệ số hai vế của đẳng thức,ta có:(dùng dấu ngoặc nhọn nha bạn)
a=1 a=1
ac+b=0 =>(dấu ngoặc nhọn) c=-2
a+cb=-3 b=2
b=2 (cái tính kết quả bạn có thế tính rõ hơn,mình làm hơi tắt)
Vậy a=1,b=2,c=-2 thì thỏa mãn đẳng thức đã cho
(Nếu không hiểu các bạn có thể xem trên google chuyên dề phương pháp hệ số bất định của bài phân tích đa thức thành nhân tử)

\(\frac{x^2}{x-1}=\frac{x^2-1+1}{x-1}=\frac{\left(x-1\right)\left(x+1\right)+1}{x-1}=x+1+\frac{1}{x-1}=x-1+\frac{1}{x-1}+2\)
Do \(x>1\) nên \(x-1>0;\frac{1}{x-1}>0\) Áp dụng bất đẳng thức Cauchy ta có :
\(x-1+\frac{1}{x-1}\ge2\sqrt{\left(x-1\right).\frac{1}{x-1}}=2\)
\(\Rightarrow x-1+\frac{1}{x-1}+2\ge4\) hay \(\frac{x^2}{x-1}\ge4\) có GTNN là 4
Dấu "=" xảy ra \(\Leftrightarrow x=2\)
Ta có \(\frac{x^2}{x-1}=\frac{x^2-1}{x-1}+\frac{1}{x-1}=x+1+\frac{1}{x-1}\)+2. Áp dụng cosi cho 2 số x+1 và 1/x-1 ta có x+1+1/x-1\(\ge\)2\(\sqrt{\left(x-1\right)\frac{1}{x-1}}=1\), suy ra biểu thức \(\ge\)3, vậy giá trị nn =3 khi x-1=1/x-1, đến đó bn giải tìm x nha
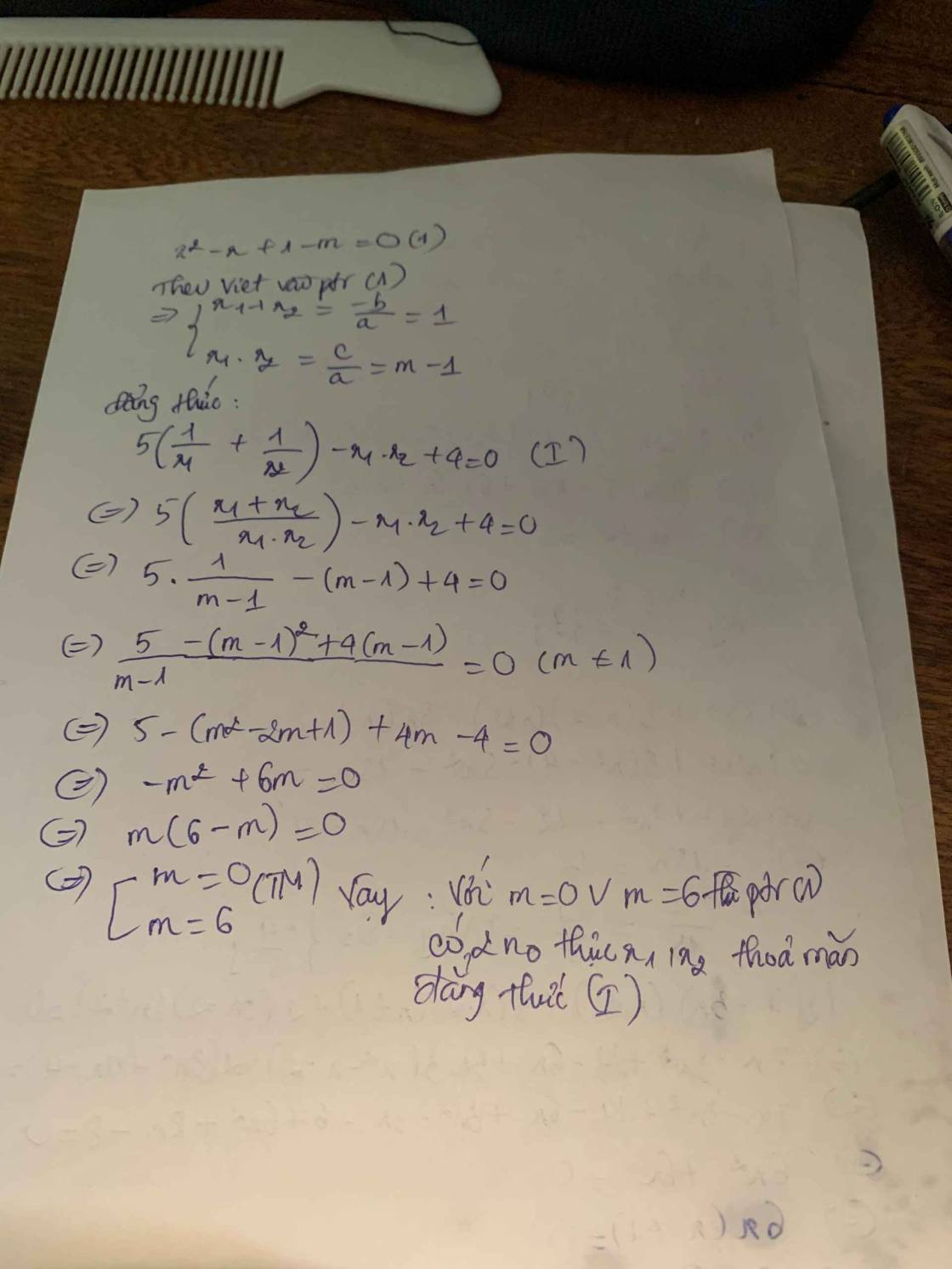

Ta có: \(3mx>x+2\Rightarrow\left(3m-1\right)x>2\left(1\right)\)
Với \(3m-1=0\Rightarrow0>2\): Vô lý nên \(3m-1\ne0.\)
Với \(3m-1>0\Leftrightarrow\Rightarrow m>\frac{1}{3}\Rightarrow x>\frac{2}{3m-1}.\)
Để (1) đúng với mọi x > 1 suy ra\(1\ge\frac{2}{3m-1}\Rightarrow\frac{2}{3m-1}-1\le0\Rightarrow\frac{3-3m}{3m-1}\le0\)
Do 3m - 1 > 0 nên \(3-3m\le0\Rightarrow m\ge1.\)
Kết hợp điều kiện suy ra \(m\ge1.\)
Với \(3m-1< 0\Leftrightarrow\Rightarrow m< \frac{1}{3}\Rightarrow x< \frac{2}{3m-1}.\)
Khi đó không xảy ra trường hợp \(\forall x>1\) thì \(x< \frac{2}{3m-1}.\)
Vậy trường hợp này loại.
Kết luận \(m\ge1.\)