Đường trung bình, đường trung trực với đường trung tuyến khác hay giống nhau ạ, nếu khác thì khác chỗ nào vậy ạaa
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


tđ của 1 đt là điểm ở chính giữa (1)
điểm ở giữa là điểm nằm trong đoạn thẳng (2)

Giả sử \(\Delta\)ABC có hai đường trung tuyến BE và CF vuông góc với nhau, AD là đường trung tuyến thứ ba. Ta cần chứng minh AD^2 = BE^2 + CF^2
Trên tia đối của tia EF lấy điểm K sao cho EF = FK
Tứ giác AKCF có hai đường chéo cắt nhau tại trung điểm E của mỗi đường nên AKCF là hình bình hành => AK//FC. Mà FC\(\perp\)BE nên BE\(\perp\)AK (*)
Ta có: F là trung điểm của AB, E là trung điểm của AC nên EF là đường trung bình của\(\Delta\)ABC => EF = 1/2BC và EF//BC hay EK//BD (1)
Mà BD = 1/2BC (gt) nên EF = BD => EK = BD (do EF = EK theo cách chọn điểm phụ) (2)
Từ (1) và (2) suy ra EKDB là hình bình hành => EB // DK (**)
Từ (*) và (**) suy ra DK \(\perp\)AK => \(\Delta\)AKD vuông tại K => AK^2 + KD^2 = AD^2 (theo định lý Py-ta-go)
Mà AK = FC (do AKCF là hình bình hành) và KD = BE (do EKDB là hình bình hành) nên AD^2 = BE^2 + CF^2 (đpcm)

Ta có : – Góc x’Oy’ và góc xOy là hai góc đối đỉnh ⇒ góc xOy = góc x’Oy’ = 90o
– ∠(xOy) và ∠(xOy’) là hai góc kề bù ⇒ ∠(xOy) + ∠(xOy’) = 180o
⇒ (xOy’) = 180o – (xOy) = 180o– 90o = 90o
– ∠(xOy’) và ∠(x’Oy) là hai góc đối đỉnh ⇒ ∠(xOy’) = ∠(x’Oy) = 90o
Khi đó các góc ∠yOx’ ; ∠x’Oy’ ; ∠y’Ox cũng đều là những góc vuông
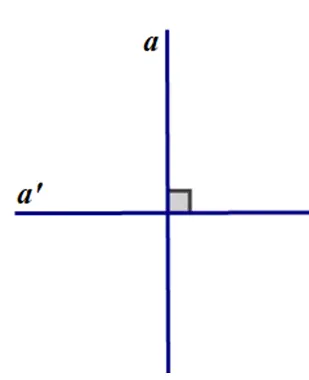
Trả lời câu hỏi Toán 7 Tập 1 Bài 2 trang 84: Vẽ phác hai đường thẳng a và a’ vuông góc với nhau và viết kí hiệu.Lời giải

\(a,\left\{{}\begin{matrix}AC=AH\left(GT\right)\\AB.chung\\\widehat{CAB}=\widehat{BAH}\left(=90^0\right)\end{matrix}\right.\Rightarrow\Delta ACB=\Delta AHB\left(c.g.c\right)\)
\(b,\left\{{}\begin{matrix}\widehat{ACB}=\widehat{CBK}\left(so.le.trong\right)\\\widehat{ABC}=\widehat{BCK}\left(so.le.trong\right)\\BC.chung\end{matrix}\right.\Rightarrow\Delta ABC=\Delta KCB\left(g.c.g\right)\Rightarrow AC=BK\left(2.cạnh.tương.ứng\right)\)
\(c,CH=AC+AH=2AC=2AB=BM\\ \left\{{}\begin{matrix}CK//AB\\AB\perp AC\end{matrix}\right.\Rightarrow CK\perp AC\Rightarrow\widehat{ACK}=90^0\\ \left\{{}\begin{matrix}BK//AC\\AC\perp AB\end{matrix}\right.\Rightarrow KB\perp AB\Rightarrow\widehat{ABK}=90^0\\ \left\{{}\begin{matrix}\widehat{ACK}=\widehat{ABK}\left(=90^0\right)\\CH=BM\left(cm.trên\right)\\AC=BK\left(cm.trên\right)\end{matrix}\right.\Rightarrow\Delta CHK=\Delta BMK\left(c.g.c\right)\)
\(d,\Delta CHK=\Delta BMK\left(cm.trên\right)\\ \Rightarrow\widehat{CKH}=\widehat{BKM}\Rightarrow\widehat{CKH}+\widehat{HKB}=\widehat{BKM}+\widehat{HKB}\\ \Rightarrow\widehat{CKB}=\widehat{HKM}\\ \Rightarrow\widehat{BAC}=\widehat{HKM}\left(\Delta ABC=\Delta KCB.nên.\widehat{CKB}=\widehat{BAC}\right)\\ \Rightarrow\widehat{HKM}=90^0\Rightarrow HK\perp KM\)

đường trung tuyến : đi qua trung điểm của cạnh
đường trung trực : đi qua trung điểm và vuông góc với cạnh
đường phân giác : chia 1 góc thành 2 góc = nhau
đường cao :hạ vuông góc từ đỉnh tới 1 cạnh
1/ Đường trung tuyến là đường đi qua trung điểm của 1 đoạn thẳng (Nó chỉ gọi là đường trung tuyến khi ở trong 1 tam giác)
2/ Đường trung trực cũng là đường đi qua trung điểm của 1 đoạn thẳng và vuông góc với đoạn thẳng đó (Nó vừa sử dụng khi nằm ngoài và trong tam giác)
3/ Đường phân giác là đường xuất phát từ một đỉnh và chi góc đó thành 2 phần bằng nhau.
4/ Đường cao là đường vuông góc với 1 đoạn thẳng (trong tam giác)



*Trong một tam giác:
- Đường trung bình là đường nối 2 trung điểm của 2 cạnh.
- Đường trung tuyến là đường nối từ 1 đỉnh đến trung điểm cạnh đối diện đỉnh đó.
- Đường trung trực là đường vuông góc tại trung điểm của 1 cạnh.