C/m giúp e với ạ, giải 1 phần nhỏ trong bài th cũng đc ạ, e cảm ơn nhìu)
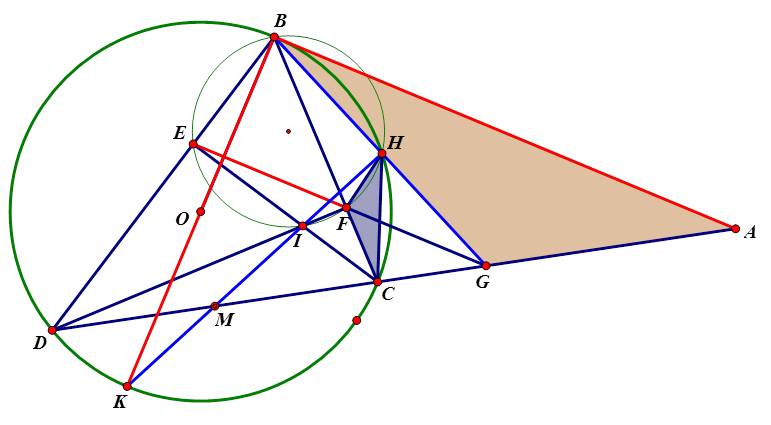
Từ điểm A nằm ngoài đường tròn (O; R) với OA > 2R. Vẽ tiếp tuyến AB và cát tuyến ACD với (O) (B là tiếp điểm; AC < AD, tia AD không cắt đoạn thẳng OB). Gọi CE, DF là các đường cao của tam giác BCD.
a) Chứng minh: tứ giác DEFC nội tiếp và EF//AB.
b) Tia EF cắt AD tại G, BG cắt (O) tại H. Chứng minh: tam giác FHC đồng dạng tam giác GAB
c) Gọi I là giao điểm của CE và DF. Tia HI cắt DC tại M. Chứng minh: OM vuông góc với CD



a: góc DEC=góc DFC=90 độ
=>DEFC nội tiếp
=>góc BFE=góc BDC=góc ABF
=>FE//AB