Cho \(a\)và \(b\)cùng dấu. Giải thích tại sao \(ab\)không thể lớn hơn hoặc bằng 0?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Em không nêu ra yêu cầu và các điều kiện liên quan của đề bài thì làm sao mn giúp em được?

A) a2+b2+c2+ab+bc+ca>=0 (*)
<=> 2a2+2b2+2c2+2ab+2bc+2ca>=0
<=> (a2+2ab+b2)+(b2+2bc+c2)+(c2+2ca+a2)>=0
<=> (a+b)2+(b+c)2+(c+a)2>=0
BĐT cuối luôn đúng với mọi a,b,c
Vậy BĐT (*) đc cm
Phần B cũng tương tự nhé
a) Ta có : a2 + b2 + c2 + ab + bc + ca = (a + b + c)2
Mà \(\left(a+b+c\right)^2\ge0\forall x\)
Nên : a2 + b2 + c2 + ab + bc + ca \(\ge0\forall x\)
b) hình như sai đề rồi bạn à !

3. abc > 0 nên trog 3 số phải có ít nhất 1 số dương.
Vì nếu giả sử cả 3 số đều âm => abc < 0 => trái giả thiết
Vậy nên phải có ít nhất 1 số dương
Không mất tính tổng quát, giả sử a > 0
mà abc > 0 => bc > 0
Nếu b < 0, c < 0:
=> b + c < 0
Từ gt: a + b + c < 0
=> b + c > - a
=> (b + c)^2 < -a(b + c) (vì b + c < 0)
<=> b^2 + 2bc + c^2 < -ab - ac
<=> ab + bc + ca < -b^2 - bc - c^2
<=> ab + bc + ca < - (b^2 + bc + c^2)
ta có:
b^2 + c^2 >= 0
mà bc > 0 => b^2 + bc + c^2 > 0
=> - (b^2 + bc + c^2) < 0
=> ab + bc + ca < 0 (vô lý)
trái gt: ab + bc + ca > 0
Vậy b > 0 và c >0
=> cả 3 số a, b, c > 0
1.a, Ta có: \(\left(a+b\right)^2\ge4a>0\)
\(\left(b+c\right)^2\ge4b>0\)
\(\left(a+c\right)^2\ge4c>0\)
\(\Rightarrow\left[\left(a+b\right)\left(b+c\right)\left(a+c\right)\right]^2\ge64abc\)
Mà abc=1
\(\Rightarrow\left[\left(a+b\right)\left(b+c\right)\left(a+c\right)\right]^2\ge64\)
\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(a+c\right)\ge8\left(đpcm\right)\)

Bởi vì ta có tính chất:
`a>=b>0=>1/a<=1/b`
GTLN bởi vì có dấu `<=`

a) x \(\in\)B(3) = {0;3;6;9;12;15;18;21;24...;63;66;...}
Mà \(21\le x\le65\)=> x \(\in\){21;24;...;63}
b) x \(⋮\)17 => x \(\in\)B(17) = {0;17;34;51;68;...}
Mà \(0\le x\le60\)=> x \(\in\){0;17;34;51}
c) x \(\in\)Ư(30) = {1;2;3;5;6;10;15;30}
Mà \(x\ge0\)=> x \(\in\){1;2;3;5;6;10;15;30}
d) \(x⋮7\)=> x \(\in\)B(7) = {0;7;14;21;28;35;42;49;56;...}
Mà \(x\le50\)thì loại bỏ số 56 ta được các số còn lại
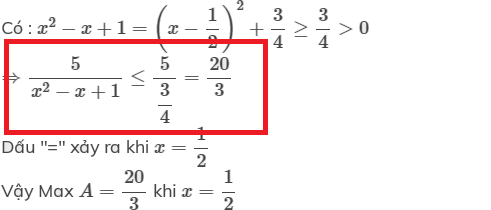
sử dụng phản chứng để chứng minh:
a và b cùng dấu => ab>=0
vậy ab lớn hơn hoặc bằng 0 với mọi a và b cùng dấu
:))