Tìm những giá trị nguyên của x: P= x2+2x-4/x+2 có giá trị là 1 số nguyên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 12 2020
ĐKXĐ: \(x\ne1\)
Ta có: \(B=\dfrac{x^4-2x^3-3x^2+8x-1}{x^2-2x+1}\)
\(=\dfrac{x^4-2x^3+x^2-4x^2+8x-4+3}{x^2-2x+1}\)
\(=\dfrac{x^2\left(x^2-2x+1\right)-4\left(x^2-2x+1\right)+3}{x^2-2x+1}\)
\(=\dfrac{\left(x-1\right)^2\cdot\left(x^2-4\right)+3}{\left(x-1\right)^2}\)
\(=x^2-4+\dfrac{3}{\left(x-1\right)^2}\)
Để B nguyên thì \(3⋮\left(x-1\right)^2\)
\(\Leftrightarrow\left(x-1\right)^2\inƯ\left(3\right)\)
\(\Leftrightarrow\left(x-1\right)^2\in\left\{1;3;-1;-3\right\}\)
mà \(\left(x-1\right)^2>0\forall x\) thỏa mãn ĐKXĐ
nên \(\left(x-1\right)^2\in\left\{1;3\right\}\)
\(\Leftrightarrow x-1\in\left\{1;9\right\}\)
hay \(x\in\left\{2;10\right\}\) (nhận)
Vậy: \(x\in\left\{2;10\right\}\)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
15 tháng 8 2023
\(A=\left(2x+1\right)\left(x^2+1\right)+\dfrac{4}{2x+1}\) (chia đa thức)
Để A nguyên \(\Rightarrow4⋮2x+1\Rightarrow\left(2x+1\right)=\left\{-4;-2;-1;1;2;4\right\}\)
\(\Rightarrow x=\left\{-\dfrac{5}{2};-\dfrac{3}{2};-1;0;\dfrac{1}{2};\dfrac{3}{2}\right\}\)
x thỏa mãn đk đề bài là \(x=\left\{-1;0\right\}\)
14 tháng 2 2018
Để \(A\) là số nguyên thì \(\left(6x-4\right)⋮\left(2x+1\right)\)
Ta có :
\(6x-4=6x+3-7=3\left(2x+1\right)-7\) chia hết cho \(2n+1\) \(\Rightarrow\) \(\left(-7\right)⋮\left(2x+1\right)\) \(\Rightarrow\) \(\left(2x+1\right)\inƯ\left(-7\right)\)
Mà \(Ư\left(-7\right)=\left\{1;-1;7;-7\right\}\)
Suy ra :
| \(2x+1\) | \(1\) | \(-1\) | \(7\) | \(-7\) |
| \(x\) | \(0\) | \(-1\) | \(3\) | \(-4\) |
Vậy \(x\in\left\{0;-1;3;-4\right\}\)
Năm mới zui zẻ nhá ^^
CM
16 tháng 8 2018
Hướng dẫn giải:
Điều kiện xác định của phân thức: x ≠ 1
Ta có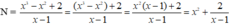 
Để N nguyên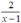 
nguyên ⇒ x - 1 là ước của 2
Ư ( 2 ) = 1 ; - 1 ; 2 ; - 2
x – 1 = 1 ⇒ x =2 (thỏa mãn điều kiện xác định);
x - 1 = -1 ⇒ x = 0 (thỏa mãn điều kiện xác định);
x - 1 = 2 ⇒ x = 3 (thỏa mãn điều kiện xác định);
x - 1 = -2 ⇒ x = -1 (thỏa mãn điều kiện xác định);
Vậy với x ∈ { -1;0;2;3 } thì phân thức N nhận giá trị nguyên
CM
21 tháng 11 2017
Chọn đáp án B
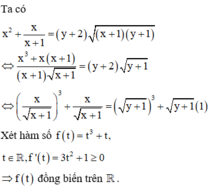
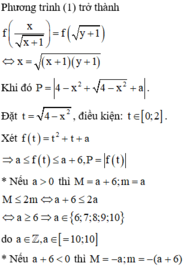
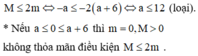
Vậy có 5 giá trị nguyên của m thỏa mãn điều kiện.
CM
9 tháng 2 2018
Hướng dẫn giải:
Điều kiện xác định của phân thức: x ≠ 2
Ta có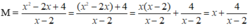 
Để M nguyên, x nhận giá trị nguyên và x - 2 là ước của 4
Ư ( 4 ) = 1 ; - 1 ; 2 ; - 2 ; 4 ; - 4
x - 2 = 1 ⇒ x = 3 (thỏa mãn điều kiện xác định);
x – 2 = -1 ⇒ x = 1 (thỏa mãn điều kiện xác định);
x – 2 = 2 ⇒ x = 4 (thỏa mãn điều kiện xác định);
x - 2 = -2 ⇒ x = 0 (thỏa mãn điều kiện xác định);
x – 2 = 4 ⇒ x = 6 (thỏa mãn điều kiện xác định);
x – 2 = -4 ⇒ x = -2 (thỏa mãn điều kiện xác định);
Vậy với x ∈ {-2; 0; 1; 3; 4; 6} thì giá trị phân thức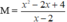 
là nguyên
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 12 2020
\(C=\dfrac{\left(x^2+3x\right)\left(x^2+2\right)-2}{x^2+2}=x^2+3x-\dfrac{2}{x^2+2}\)
\(C\in Z\Leftrightarrow2⋮\left(x^2+2\right)\)
\(\Leftrightarrow x^2+2=2\Rightarrow x=0\)