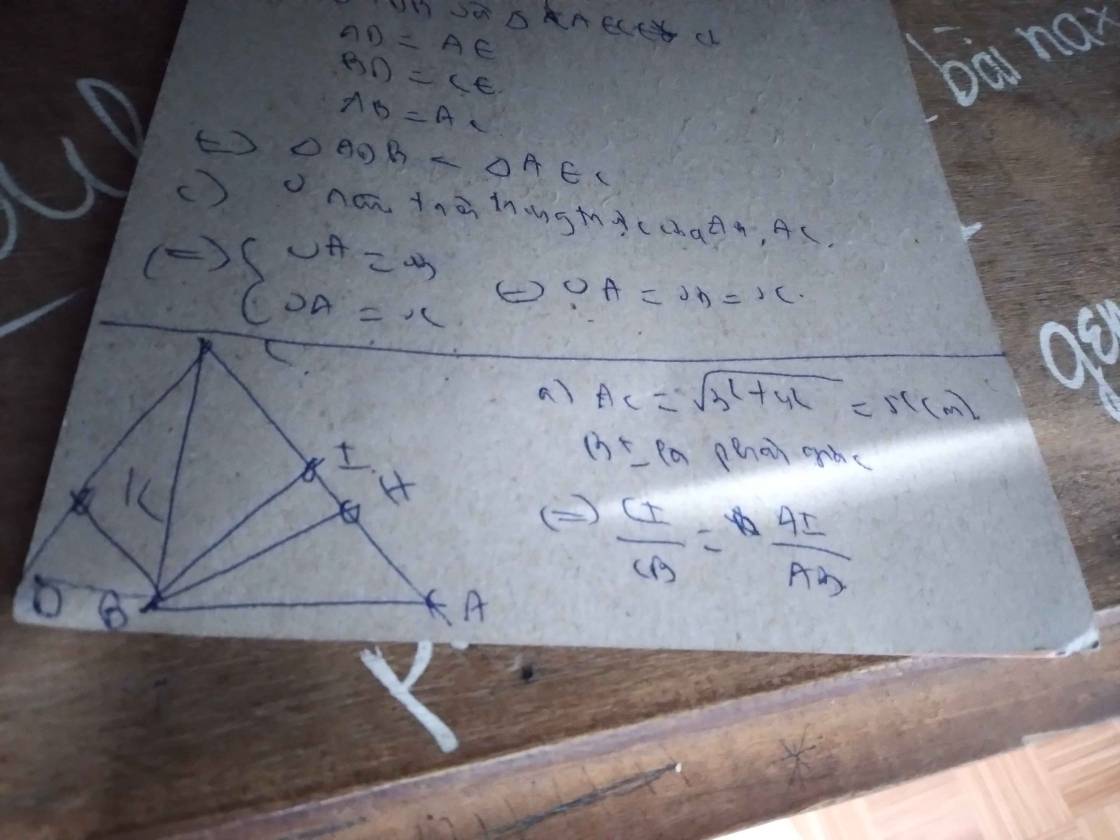
Cho ∆ABC vuông tại A có AB = 3cm, AC = 4cm, đường cao AH và tia phân giác BD (D ∈ AC) của góc B cắt nhau tại I
a) C/m: IA × BH = IH × BA
b) C/m: AB² = BH × BC. Tính AH, CH.
c) C/m: HI × DC = AD × AI
d) Qua B kẻ đường thẳng song song với AC cắt đường thẳng AH tại E. Tính BE.

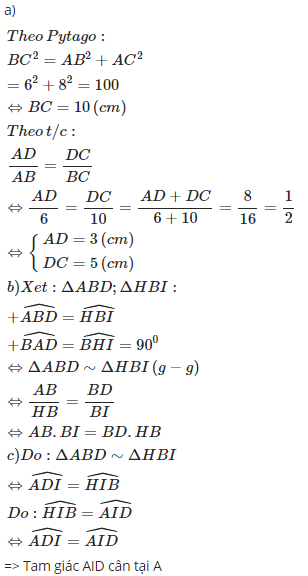

a: Xét ΔBAH có BI là phân giác
nên IA/BA=IH/BH
=>IA*BH=BA*IH
b: ΔACB vuông tạiA có AH vuông góc BC
nên BA^2=BH*BC
\(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
AH=3*4/5=2,4cm
CH=4^2/5=3,2cm
c: ΔBAC có BD là phân giác
nên DC/DA=BC/BA
=>DC/DA=BA/BH=AI/IH
=>DC*IH=DC*IA