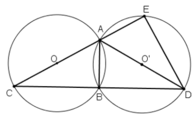
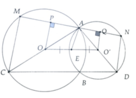
Cho hai dường tròn (O) và (O) cắt nhau tại A và B. Vẽ các đường kính AOC và AOO'D.Dường thẳng AC cắt đường tròn (O) tại E. Dường thẳng AD cắt đường tròn (O) tại F. Chứng minh rằng: a. Ba điểm C, B, D thẳng hàng. b. Tứ giác CDEF nội tiếp. C. A là tâm đường tròn (hoặc bàng tiếp)của tam giác BEE.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
23 tháng 10 2019
Vì A,B,C ∈ (O)
⇒ BO = OA = OC
⇒ BO = AC/2.
Tam giác ABC có đường trung tuyến BO và BO bằng một phần hai độ dài cạnh tương ứng AC
=> Tam giác ABC là tam giác vuông tại B ( định lí)
⇒ 
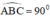
Chứng minh tương tự
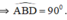
Đường tròn tâm O và O’ bằng nhau ⇒ AC = AD.(AC,AD lần lượt là bán kính của (O) và (O’))
Xét hai tam giác vuông ΔABC và ΔABD có:
AB chung, AC = AD
⇒ ΔABC = ΔABD (cạnh huyền – cạnh góc vuông)
⇒ BC = BD(hai cạnh tương ứng)
⇒ 
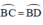( định lý )
CM
22 tháng 7 2019
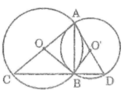
Tam giác ABC nội tiếp trong đường tròn (O) có AC là đường kính nên góc (ABC) = 90 °
Tam giác ABD nội tiếp trong đường tròn (O’) có AD là đường kính nên góc (ABD) = 90 °
Ta có: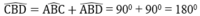
Vậy ba điểm C, B, D thẳng hàng và AB ⊥ CD
26 tháng 6 2021
a) Xét tứ giác SAOB có
\(\widehat{SAO}+\widehat{SBO}=180^0\left(90^0+90^0=180^0\right)\)
nên SAOB là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Xét (O) có
SA là tiếp tuyến có A là tiếp điểm(gt)
SB là tiếp tuyến có B là tiếp điểm(gt)
Do đó: SA=SB(Tính chất hai tiếp tuyến cắt nhau)
Ta có: SA=SB(cmt)
nên S nằm trên đường trung trực của AB(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: OA=OB(=R)
nên O nằm trên đường trung trực của AB(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra SO là đường trung trực của AB
hay SO\(\perp\)AB(Đpcm)
AT
28 tháng 6 2021
b) đề phải là \(SA^2=SD.SE\) chứ SD không bằng SE sao \(SD^2=SD.SE\) được
Vì AE là đường kính \(\Rightarrow\angle ADE=90\) mà \(\angle SAE=90\)
\(\Rightarrow\Delta SAE\) vuông tại A có AD là đường cao
\(\Rightarrow SA^2=SD.SE\)
c) Trong (O) có DE là dây cung không đi qua O và I là trung điểm DE
\(\Rightarrow OI\bot DE\Rightarrow\angle OIS=90\Rightarrow\angle OIS=\angle OBS=90\)
\(\Rightarrow OIBS\) nội tiếp mà SAOB nội tiếp (câu a)
\(\Rightarrow O,I,A,S,B\) cùng thuộc 1 đường tròn
\(\Rightarrow AIBS\) nội tiếp \(\Rightarrow\angle AIS=\angle ABS=\angle SAB\) (\(\Delta SAB\) cân tại S)
Xét \(\Delta SAK\) và \(\Delta SIA:\) Ta có: \(\left\{{}\begin{matrix}\angle SIA=\angle SAK\\\angle ISAchung\end{matrix}\right.\)
\(\Rightarrow\Delta SAK\sim\Delta SIA\left(g-g\right)\Rightarrow\dfrac{SA}{SI}=\dfrac{SK}{SA}\Rightarrow SA^2=SK.SI\)
mà \(SA^2=SD.SE\Rightarrow SD.SE=SK.SI\)
d) AB cắt OI tại F'
Vì AE là đường kính \(\Rightarrow\angle ABE=90\Rightarrow F'BE=90\)
\(\Rightarrow\angle F'BE=\angle F'IE\Rightarrow F'BIE\) nội tiếp \(\Rightarrow\angle ABI=\angle F'EI\)
mà \(\angle ABI=\angle ASI\) (AIBS nội tiếp) \(=\angle ASE\)
\(\Rightarrow\angle F'EI+\angle AES=\angle ASE+\angle AES=90\)
\(\Rightarrow\angle F'EO=90\Rightarrow EF'\) là tiếp tuyến \(\Rightarrow\) đpcm
CM
20 tháng 10 2019
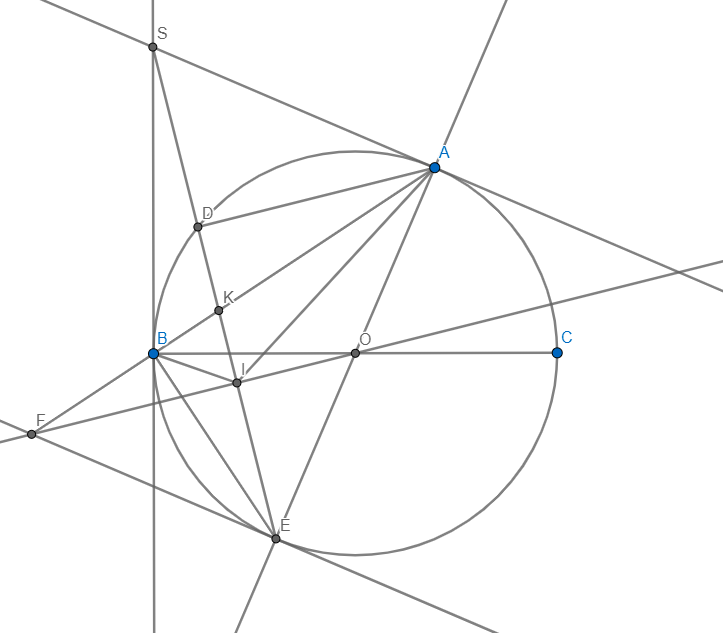
a, Chú ý: C M A ^ = D N A ^ = 90 0
b, Vẽ OP ⊥ MA; O'Q ⊥ NA
Chú ý hình thang vuông OPQO’ có EA là đường trung bình
CM
17 tháng 1 2019
a. b.
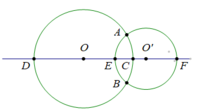
c. - Đường tròn (O’; 1cm) có đường kính là: EF; Các dây cung là: EA, EB, AB, FA, FB
Vì E thuộc (O’; 1cm) nên EO’=1cm; EF=2.EO’=2cm
- Đường tròn (O; 1,5cm) có đường kính là: DC; Các dây cung là: DA, DB, AB, AC, CB
Vì C thuộc (O; 1,5cm) nên CO=1,5cm; DC=2.CO=3cm
d. Vì đường tròn (O’; 1cm) cắt đoạn thẳng OO’ tại E, nên E nằm giữa 2 điểm O và O’.
Ta có: O E + E O ' = O O ' ⇒ O E = 1 c m
Mà EO’=1cm, nên OE=EO’ (=1cm)
Do đó: E là trung điểm của đợn thẳng OO’.
e. Vì đường tròn (O; 1cm) cắt đường thẳng OO’ tại D, đường tròn (O’; 1cm) cắt đường thẳng OO’ tại F, nên 4 điểm D, O, O’, F lần lượt theo thứ tự đó và DO=1,5cm; O’F=1cm.
Ta có: D F = D O + O O ' + O ' F = 1 , 5 + 2 + 1 = 4 , 5 c m .
Vậy DF=4,5cm
a: góc ABC=1/2*sđ cung AC=90 độ
góc ABD=1/2*180=90 độ
góc CBD=góc ABC+góc ABD=90+90=180 độ
=>C,B,D thẳng hàng
b: góc AFC=1/2*sđ cung AC=90 độ
=>CF vuông góc AD
góc AED=1/2*180=90 độ
=>DE vuông góc AC
góc CED=góc CFD=90 độ
=>CEFD nội tiếp