Cho số phức z = a − 2 + (b + 1)i với a, b ∈ Z và |z| = 2. Tìm giá trị lớn nhất của biểu thức S = a + 2b.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

CM
25 tháng 7 2017
Đáp án D
Phương pháp giải:
Đặt z=a+bi thực hiện yêu cầu bài toán, chú ý số phức là số thực khi phần ảo bằng 0
Lời giải:
Ta có ![]()
Khi đó
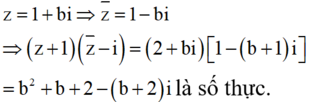
Khi và chỉ khi b + 2 = 0 ⇔ b = - 2
Vậy S=a+2b= -3

CM
17 tháng 2 2019
Với ![]()
![]() Khi đó
Khi đó
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Dấu bằng đạt tại
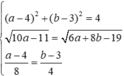
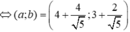
⇒ a - 2 b = - 2
Chọn đáp án B.
Mẹo trắc nghiệm: Có
![]()
![]()
![]()
Khi đó
![]()
![]()
![]()
![]()
![]()
Khi đó a-2b![]()
Chọn đáp án B.

CM
9 tháng 7 2019
Chọn đáp án B.
Cách 1: (Sử dụng kiến thức Hình học)
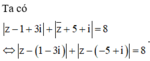
Gọi M, A, B, I lần lượt là điểm biểu diễn cho các số phức
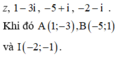
Có I là trung điểm của đoạn thẳng AB và

Áp dụng bất đẳng thức Cô-si, ta có


Cách 2: (Sử dụng kiến thức Đại số)
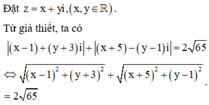
Áp dụng bất đẳng thức Bu-nhi-a-cốp-xky, ta có
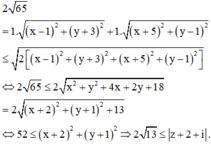
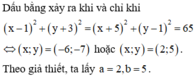

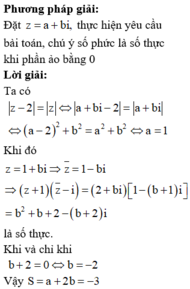

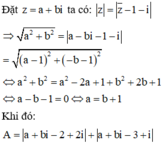
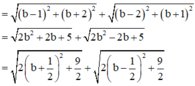
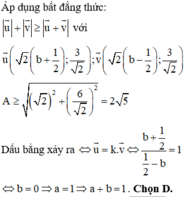

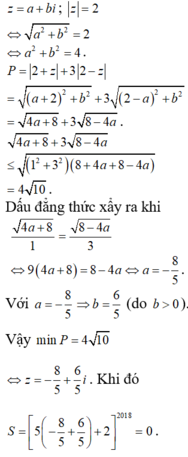
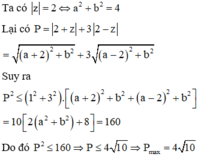
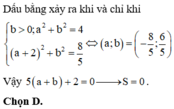
Lời giải:
Ta có:
$\sqrt{(a-2)^2+(b+1)^2}=2$
$\Rightarrow (a-2)^2+(b+1)^2=4$
Áp dụng BĐT Bunhiacopxky:
$[(a-2)^2+(b+1)^2](1^2+2^2)\geq [(a-2)+2(b+1)]^2$
$\Leftrightarrow 20\geq (a+2b)^2$
$\Rightarrow a+2b\leq \sqrt{20}$
Vậy $S_{\max}=\sqrt{20}$