Ví dụ 1: Cho hai điểm A và B thuộc tia Oz sao cho OA = 1cm; OB = 3cm. C là điểm thuộc tia đối
của tia Oz sao cho OC = 1cm. Chọn câu trả lời đúng nhất:
A. Điểm A là trung điểm của đoạn thẳng BC.
B. Điểm O là trung điểm của đoạn thẳng AC.
C. Điểm O là trung điểm của đoạn thẳng BC.
D. A và O lần lượt là trung điểm của BC và AC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

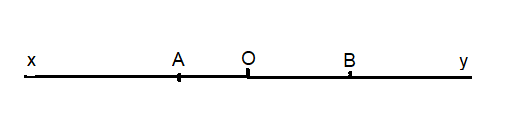
a. Trong ba điểm O;A;B điểm O nằm giữa 2 điểm còn lại
b. Ta có : OA + OB = AB
hay 3 + 4 = AB
=> AB= 7(cm)
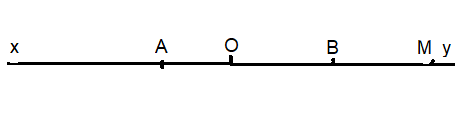
C. Vì B là trung điểm OM nên OB = BM = OM/2 (cm)
mà OB = 4 cm => BM = 4cm
Ta có : OB + BM = OM
Hay 4 + 4 =OM
=> OM = 8(cm)
@Liz.Ald2094

b) B,M thuộc tia Ox
OB>OM ( 5>1)
=> B nằm giữa O,M
=> OB+BM=OM
=> 5+ 1= OM
=> Om=6 cm

a: Xét ΔOAI và ΔOBI có
OA=OB
\(\widehat{AOI}=\widehat{BOI}\)
OI chung
Do đó: ΔOAI=ΔOBI
\(a,\left\{{}\begin{matrix}OA=OB\\\widehat{AOI}=\widehat{BOI}\\OI\text{ chung}\end{matrix}\right.\Rightarrow\Delta AOI=\Delta BOI\left(c.g.c\right)\\ b,\text{Gọi }AB\cap OI=\left\{H\right\}\\ \left\{{}\begin{matrix}OA=OB\\\widehat{AOI}=\widehat{BOI}\\OH\text{ chung}\end{matrix}\right.\Rightarrow\Delta AOH=\Delta BOH\left(c.g.c\right)\\ \Rightarrow\widehat{AHO}=\widehat{BHO}\\ \text{Mà }\widehat{AHO}+\widehat{BHO}=180^0\\ \Rightarrow\widehat{AHO}=\widehat{BHO}=90^0\\ \Rightarrow OI\bot AB\)

a: Xét ΔOAC và ΔOBC có
OA=OB
\(\widehat{AOC}=\widehat{BOC}\)'
OC chung
Do đó: ΔOAC=ΔOBC
=>AC=BC và \(\widehat{OAC}=\widehat{OBC}\)
\(\widehat{OAC}+\widehat{xAC}=180^0\)(hai góc kề bù)
\(\widehat{OBC}+\widehat{yBC}=180^0\)(hai góc kề bù)
mà \(\widehat{OAC}=\widehat{OBC}\)
nên \(\widehat{xAC}=\widehat{yBC}\)
b: OA=OB
=>O nằm trên đường trung trực của AB(1)
CA=CB
=>C nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra OC là đường trung trực của AB
=>OC\(\perp\)AB
=>Oz\(\perp\)AB
Chọn C