giải các bất phương trình sau và biểu diễn nghiệm trêm trục số
2x+3(x-2)<5x-(2x-4)
làm ơn giải từng bước cho mk vs cảm ơn nhìu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: 2x-1>=5
nên 2x>=6
hay x>=3
b: \(\dfrac{x-2}{3}>=x-\dfrac{x-1}{2}\)
=>2x-4>=6x-3(x-1)
=>2x-4>=6x-3x+3
=>2x-4>=3x+3
=>-x>=7
hay x<=-7
a.\(2x-1\ge5\)
\(\Leftrightarrow2x\ge6\)
\(\Leftrightarrow x\ge3\)
Vậy \(S=\left\{x|x\ge3\right\}\)
b.\(\dfrac{x-2}{3}\ge x-\dfrac{x-1}{2}\)
\(\Leftrightarrow\dfrac{2\left(x-2\right)}{6}\ge\dfrac{6x-3\left(x-1\right)}{6}\)
\(\Leftrightarrow2\left(x-2\right)\ge6x-3\left(x-1\right)\)
\(\Leftrightarrow2x-4\ge6x-3x+3\)
\(\Leftrightarrow-x\ge7\)
\(\Leftrightarrow x\le7\)
Vậy \(S=\left\{x|x\le7\right\}\)

d: =>-2x<=1
=>x>=-1/2
e: =>3x<=10
=>x<=10/3
f: =>2x-6+12<=x+2
=>2x+6<=x+2
=>x<=-4

`(x-2)/6 -(x-1)/3 < x/2`
`<=> (x-2)/6 -(2(x-1))/6 < (3x)/6`
`<=> x-2 - (2x-2) <3x`
`<=> x-2-2x+2<3x`
`<=> -x <3x`
`<=> -x-3x<0`
`<=> -4x<0`
`<=> x>0`
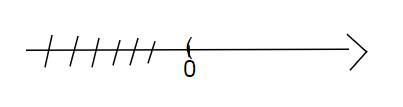

\(\dfrac{x-2}{2}+1\le\dfrac{x-1}{3}\)
\(\Leftrightarrow\dfrac{3\left(x-2\right)}{6}+\dfrac{1.6}{6}\le\dfrac{2\left(x-1\right)}{6}\)
`<=> 3x - 6 + 6 <= 2x-2`
`<=> 3x <= 2x-2`
`<=> 3x -2x <= -2`
`<=> x <= -2`
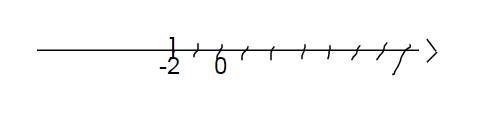
\(\dfrac{x-2}{2}\)+1≤\(\dfrac{x-1}{3}\)
<=>\(\dfrac{3x-6}{6}\)+\(\dfrac{6}{6}\)≤\(\dfrac{2x-1}{6}\)
<=>3x-6+6≤2x-1
<=>x<-1

Ta có: \(x^2< 9\)
\(\Leftrightarrow\left\{{}\begin{matrix}-3< x\\x< 3\end{matrix}\right.\Leftrightarrow-3< x< 3\)

\(x^2-4x+3\ge0\)
\(\left(x-1\right)\left(x-3\right)\ge0\)
TH1; X-1>=0 VA X-3>=0
TH2: X-1=<0 VA X-3<=0
Vay x>=3 hoac x<=1
\(2x+3\left(x-2\right)< 5x-\left(2x-4\right)\)
<=>\(2x+3x-6< 5x-2x+4\)
<=>\(2x+3x-5x+2x< 10\)
<=>\(2x< 10\)
<=>x<5