cứu tui cứu tui
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{EAC}\) chung
Do đó: ΔADB\(\sim\)ΔAEC(g-g)

a) Có góc A chung và 2 góc vuông => ĐPCM
b) Xét EHB và DHC có:
2 góc vuông và 2 góc đối đỉnh EHB và DHC
=> EHB đồng dạng với DHC
=>BH/CH=EH/DH
=>BH.DH=EH.CH
c)Từ câu a ta suy ra được tỉ số : AB/AC=AD/AE
và có góc A chung .
Từ đó suy ra: ADE đồng dạng với ABC
=> góc ADE= góc ABC
d) Ta có IO là đường trung bình ( tự chứng minh )
=> IO//AH => AHM đồng dạng với IOM
Tỉ số cạnh = AM/IM =2 ( do là đường trung bình )
Tỉ số diện tích của AHM so với IOM là 22=4
Vậy SAHM=4.SIOM

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc DAB chung
=>ΔADB đồng dạng với ΔAEC
=>AD/AE=AB/AC
=>AD/AB=AE/AC
=>ΔADE đồng dạng vơi ΔABC
b: Xet ΔHEB vuông tại E và ΔHDC vuông tại D co
góc EHB=góc DHC
=>ΔHEB đồng dạng vơi ΔHDC
=>HE/HD=HB/HC
=>HE*HC=HB*HD
Xét tứ giác BHCK co
BH//CK
BK//CH
=>BHCK là hình bình hành
=>BC cắt HK tại trung điểm của mỗi đường
=>H,M,K thẳng hàng
ΔAED đồg dạng với ΔACB
=>góc AED=góc ACB
d: Xét ΔBEC vuông tại E và ΔBOA vuông tại O có
góc EBC chung
=>ΔBEC đồng dạng với ΔBOA
=>BE/BO=BC/BA
=>BE*BA=BO*BC
Xét ΔCDB vuông tại D và ΔCOA vuông tại O có
góc OCA chung
=>ΔCDB đồng dạng với ΔCOA
=>CD/CO=CB/CA
=>CO*CB=CD*CA
=>BE*BA+CD*CA=BC^2

Hình (tự vẽ)
a) Xét \(\Delta ABDva\Delta ACE\):
\(\widehat{A}\left(chung\right)\)
\(\widehat{E}=\widehat{D}\left(=90'\right)\)
\(=>\Delta ABD\)đồng dạng \(\Delta ACE\left(g-g\right)\)
\(=>\frac{AB}{AC}=\frac{AD}{AE}< =>AB.AE=AC.AD\)
b)xét \(\Delta ADEva\Delta ABC\)
\(\widehat{A}\left(chung\right)\)
\(\frac{AB}{AC}=\frac{AD}{AE}\)
\(=>\Delta ADE\)đồng dạng \(\Delta ABC\left(c-g-c\right)\)
c)Lưu Ý! Đề phải là DE cắt CB tại I
CM:
\(\widehat{IEB}=\widehat{AED}\)(đối đỉnh)
\(\widehat{AED}=\widehat{ACB}\)(tam giác ADE đồng dạng với tam giác ABC)
\(=>\widehat{IEB}=\widehat{ACB}\)
Lại có góc I chung
\(=>\Delta IBE\) đồng dạng với \(\Delta IDC\left(g-g\right)\)
d) từ c)=>\(\frac{IB}{ID}=\frac{IE}{IC}< =>ID.IE=IB.IC=\left(OI-OB\right)\left(OI+OC\right)\)
Mà OC=OB(gt)
\(=>ID.IE=\left(OI+OC\right)\left(OI-OC\right)=OI^2-OC^2\)

c: Xét tứ giác BHCK có
BH//CK
BK//CH
=>BHCK là hbh
=>M là trung điểm của HK
=>H,M,K thẳng hàng
d: BACK là hình thoi
=>M là trung điểm của AK và AK vuông góc BC
=>A,H,M thẳng hàng
=>ΔABC cân tại A
=>AB=AC
tham khảo
a.Ta có BK//CH(⊥AB),CK//BH(⊥AC)BK//CH(⊥AB),CK//BH(⊥AC)
→BHCK→BHCK là hình bình hành
b.Vì BHCKBHCK là hình bình hành
→HK∩BC→HK∩BC tại trung điểm mỗi đường
Do MM là trung điểm BCBC
→M→M là trung điểm HKHK
→H,M,K→H,M,K thẳng hàng
c.Ta có O,MO,M là trung điểm AK,HKAK,HK
→OM→OM là đường trung bình ΔAHKΔAHK
→OM//AH→OM//AH
Do BD∩CE=H→HBD∩CE=H→H là trực tâm ΔABC→AH⊥BCΔABC→AH⊥BC
→OM⊥BC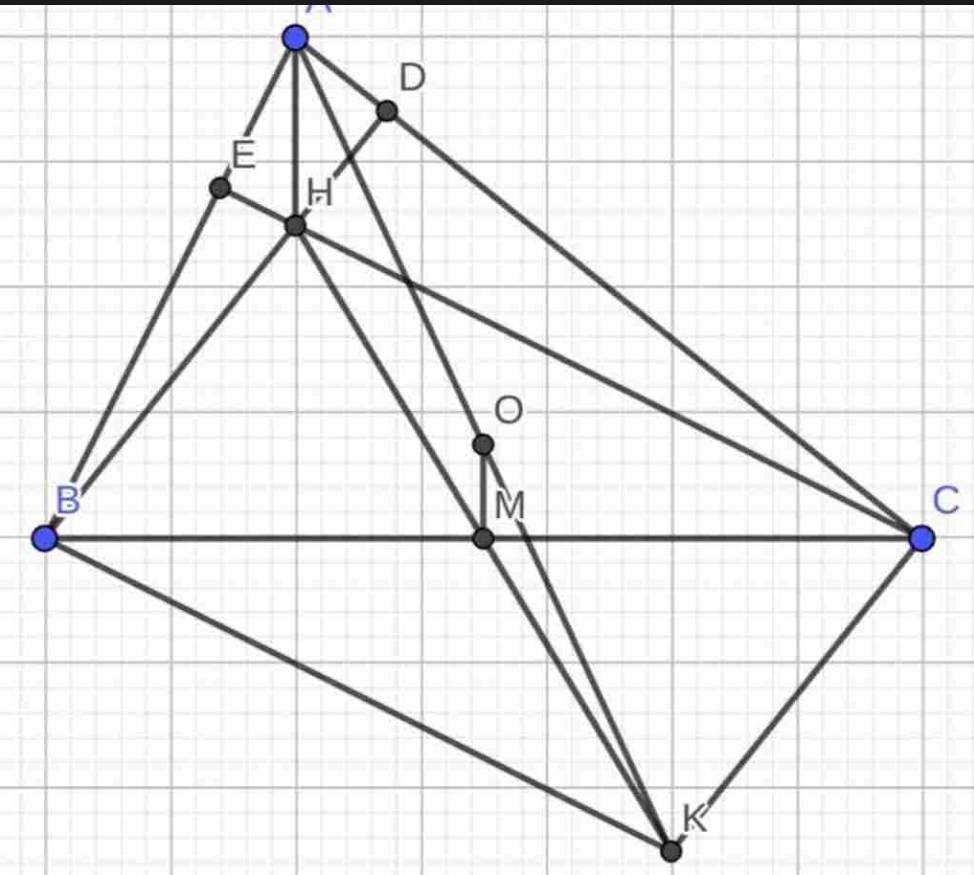

a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
góc A chung
=>ΔABD đồng dạng với ΔACE
b: ΔABD đồng dạng với ΔACE
=>AD/AE=AB/AC
=>AD/AB=AE/AC
=>ΔADE đồng dạng với ΔABC
=>góc ADE=góc ABC

Bài 1:
a) Xét tam giác ABE và tam giác ACF có:
Góc AEB=góc AFC(=90 độ)
Góc A chung
=>Tam giác ABE đồng dạng vs tam giác ACF (g-g)
b)
Vì tam giác ABE đồng dạng vs tam giác ACF(cmt)
=>\(\frac{AB}{AC}=\frac{AE}{AF}\)
Xét tam giác AFE và tam giác ACB có:
Góc A chung(gt)
\(\frac{AB}{AC}=\frac{AE}{AF}\)
=>Tam giác AFE và tam giác ACB đồng dạng (c-g-c)
c)
H ở đou ra vại? :))

a: Xet ΔHEB vuông tại E và ΔHDC vuông tại D có
góc EHB=góc DHC
=>ΔHEB đồng dạng với ΔHDC
b: góc BEC=góc BDC=90 độ
=>BEDC nội tiếp
=>góc DEC=góc DBC
c: ΔEBC vuông tại E
mà EO là trung tuyến
nên EO=BC/2
ΔDBC vuông tại D
mà DO là trung tuyến
nên DO=BC/2=EO
=>ΔDOE cân tại O