Trong mặt phẳng toạ độ Oxy cho (d):y=3x+m-2 Tìm m để (d) cắt (d1):y=-2x+6m+3 tại một điểm thuộc đường tròn (O) bán kính là 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 5 2023
a: PTHĐGĐ là:
x^2-2x-|m|-1=0
a*c=-|m|-1<0
=>(d)luôn cắt (P) tại hai điểm phân biệt
b: Bạn bổ sung lại đề đi bạn
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
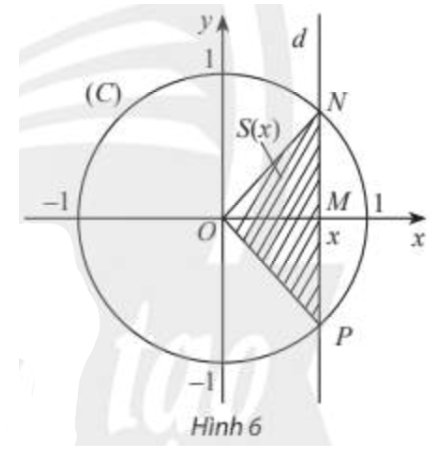
a) Ta có: \(\left( C \right):{x^2} + {y^2} = 1 \Leftrightarrow y = \pm \sqrt {1 - {x^2}} \).
Độ dài \(OM\) chính là giá trị tuyệt đối của hoành độ của điểm \(M\). Vậy \(OM = \left| x \right|\).
Độ dài \(MN\) chính là giá trị tuyệt đối của tung độ của điểm \(N\). Vậy \(MN = \left| {\sqrt {1 - {x^2}} } \right| = \sqrt {1 - {x^2}} \).
\(S\left( x \right) = {S_{ONP}} = \frac{1}{2}.NP.OM = MN.OM = \sqrt {1 - {x^2}} .\left| x \right|\).
b) Xét hàm số \(S\left( x \right) = \sqrt {1 - {x^2}} .\left| x \right| = \left\{ {\begin{array}{*{20}{c}}{x\sqrt {1 - {x^2}} }&{khi\,\,0 \le x \le 1}\\{ - x\sqrt {1 - {x^2}} }&{khi\,\, - 1 \le x < 0}\end{array}} \right.\).
ĐKXĐ: \(1 - {x^2} \ge 0 \Leftrightarrow - 1 \le x \le 1\)
Hàm số \(S\left( x \right)\) có tập xác định là \(\left[ { - 1;1} \right]\).
Vậy hàm số \(S\left( x \right)\) xác định trên các khoảng \(\left( { - 1;0} \right)\) và \(\left( {0;1} \right)\) nên liên tục trên các khoảng \(\left( { - 1;0} \right)\) và \(\left( {0;1} \right)\).
Ta có: \(S\left( 0 \right) = 0.\sqrt {1 - {0^2}} = 0\)
\(\mathop {\lim }\limits_{x \to {0^ + }} S\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \left( {x\sqrt {1 - {x^2}} } \right) = 0.\sqrt {1 - {0^2}} = 0\)
\(\mathop {\lim }\limits_{x \to {0^ - }} S\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} \left( { - x\sqrt {1 - {x^2}} } \right) = - 0.\sqrt {1 - {0^2}} = 0\)
Vì \(\mathop {\lim }\limits_{x \to {0^ + }} S\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} S\left( x \right) = 0\) nên \(\mathop {\lim }\limits_{x \to 0} S\left( x \right) = 0 = S\left( 0 \right)\)
Vậy hàm số \(S\left( x \right)\) liên tục tại điểm \({x_0} = 0\). Vậy hàm số \(S\left( x \right)\) liên tục trên \(\left( { - 1;1} \right)\).
c) \(\mathop {\lim }\limits_{x \to {1^ - }} S\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \left( {x\sqrt {1 - {x^2}} } \right) = 1.\sqrt {1 - {1^2}} = 0\)
\(\mathop {\lim }\limits_{x \to - {1^ + }} S\left( x \right) = \mathop {\lim }\limits_{x \to - {1^ + }} \left( { - x\sqrt {1 - {x^2}} } \right) = - 1.\sqrt {1 - {{\left( { - 1} \right)}^2}} = 0\)
25 tháng 7 2023
a: khi m=2 thì (d): y=4x-2^2+1=4x-3
PTHĐGĐ:
x^2-4x+3=0
=>x=1 hoặc x=3
Khi x=1 thì y=1
Khi x=3 thì y=9
b: PTHĐGĐ là;
x^2-2mx+m^2-1=0
Δ=(-2m)^2-4(m^2-1)=4>0
=>(P) luôn cắt (d) tại hai điểm phân biệt
2y1+4m*x2-2m^2-3<0
=>2(2mx1-m^2+1)+4m*x2-2m^2-3<0
=>4m*x1-2m^2+2+4m*x2-2m^2-3<0
=>-4m^2+4m*(x1+x2)-1<0
=>-4m^2+4m*(2m)-1<0
=>-4m^2+8m-1<0
=>\(\left[{}\begin{matrix}m< \dfrac{2-\sqrt{3}}{2}\\m>\dfrac{2+\sqrt{3}}{2}\end{matrix}\right.\)
Lời giải:
PT hoành độ giao điểm:
$3x+m-2=-2x+6m+3$
$\Leftrightarrow 5x=5m+5$
$\Leftrightarrow x=m+1$
$y=3x+m-2=3(m+1)+m-2=4m+1$
Vậy tọa độ giao điểm của $(d)$ và $(d_1)$ là $I(m+1, 4m+1)$
$I$ thuộc đường tròn $(O)$ bán kính 3
Tức là $OI=3$
$\Leftrightarrow \sqrt{(m+1)^2+(4m+1)^2}=3$
Giải pt trên suy ra $m=-1$ hoặc $m=\frac{7}{17}$