cho tam giác ABC vuông tại A trung tuyến AM .Chứng minh rằng AM=1/2BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Trên tia AM lấy điểm D sao cho DM = AM . Nối D với C . CM , tam giác MBA bằng tam giác MCD ( c . g . c )
Suy ra góc BAM bằng góc CDM , suy ra CD // BA suy ra BAC+ DCA = 180 độ và góc BAC bằng góc DCA theo CM 2 tam giác trên suy ra
BAC = DCA = 90 độ
Kết luận : Tam giác trên là tam giac vuông tại A
kết luận tam giác trên là tam giác vuông để làm j người ta cho sẵn rồi mà

Trên tia đối của tia MA, lấy điểm D sao cho MA=MD
Xét tứ giác ACDB có
M là trung điểm của đường chéo BC
M là trung điểm của đường chéo AD
Do đó: ACDB là hình bình hành
Hình bình hành ACDB có \(\widehat{CAB}=90^0\)
nên ACDB là hình chữ nhật
Suy ra: BC=AD
mà \(AM=\dfrac{1}{2}AD\)
nên \(AM=\dfrac{1}{2}BC\)

giúp mik nhanh câu c dc khum ạ
2 câu kia mik xong r
cảm ơn các bạn

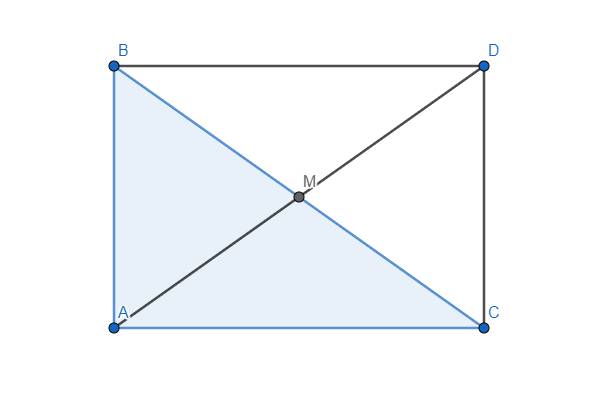
Trên tia đối của tia MA lấy điểm D sao cho \(MD=MA\). Khi đó xét 2 tam giác MAB và MDC, ta có \(MA=MD\) (cách vẽ), \(\widehat{AMB}=\widehat{DMC}\) và \(MB=MC\) (do AM là đường trung tuyến của tam giác ABC)
\(\Rightarrow\Delta MAB=\Delta MDC\left(c.g.c\right)\) \(\Rightarrow\widehat{MAB}=\widehat{MDC}\) \(\Rightarrow AB//CD\). Mà \(AB\perp AC\) nên \(AC\perp CD\) hay \(\widehat{ACD}=90^o\)
Đồng thời ta cũng có \(AB=CD\)
Xét 2 tam giác ABC và CDA, có AC là cạnh chung, \(\widehat{BAC}=\widehat{DCA}\left(=90^o\right)\) và \(AB=CD\left(cmt\right)\), suy ra \(\Delta ABC=\Delta CDA\left(c.g.c\right)\) \(\Rightarrow BC=AD\)
\(\Rightarrow\dfrac{1}{2}BC=\dfrac{1}{2}AD\) \(\Rightarrow MB=MA\)
Từ đó ta có \(MA=MB=MC=MD\), suy ra đpcm.

ΔABC vuông tại A có AM là trung tuyến
nên MA=MB
mà MA=AB
nên MA=AB=MB
=>ΔMAB đều
=>góc B=60 độ
=>góc C=90-60=30 độ
sin C=sin 30=1/2