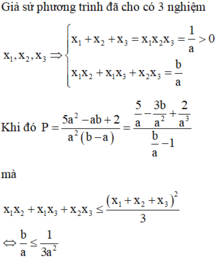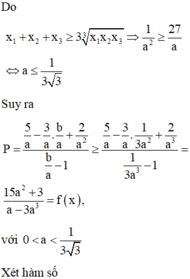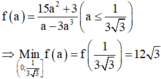Tìm a,b sao cho x4+ax3+bx-1 chia hết cho x2-1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 7 2021
\(x^4+ax^3+bx-1=\left(x^2-1\right)\left(x^2+1\right)+ax\left(x^2-1\right)+\left(a+b\right)x\)
\(\Rightarrow x^4+ax^3+bx-1\) chia hết cho \(x^2-1\) khi \(a+b=0\)
\(\Leftrightarrow b=-a\)
(Chỉ cần a; b là 2 số đối nhau là đủ, có vô số cặp a;b thỏa mãn đề bài, ví dụ (a;b)=(1;-1); (2;-2); (3;-3)... đều đúng)
HH
0
T
1
17 tháng 9 2021
\(1,A⋮B\Leftrightarrow x^3-3x^2-ax+3=\left(x-1\right)\cdot a\left(x\right)\)
Thay \(x=1\)
\(\Leftrightarrow1-3-a+3=0\\ \Leftrightarrow a=1\)
\(2,A⋮B\Leftrightarrow3x^3-16x^2+25x+a=\left(x^2-4x+3\right)\cdot b\left(x\right)\\ \Leftrightarrow3x^3-16x^2+25x+a=\left(x-3\right)\left(x-1\right)\cdot b\left(x\right)\)
Thay \(x=1\)
\(\Leftrightarrow3-16+25+a=0\\ \Leftrightarrow a=-12\)
Thay \(x=3\)
\(\Leftrightarrow3\cdot27-16\cdot9+25\cdot3+a=0\\ \Leftrightarrow81-144+75+a=0\\ \Leftrightarrow12+a=0\Leftrightarrow a=-12\)
Vậy \(a=-12\)
CM
25 tháng 3 2019
Giả sử phương trình đã cho có 3 nghiệm
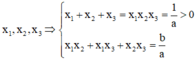
Khi đó
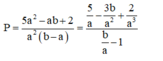
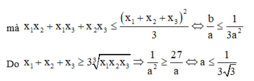
Suy ra
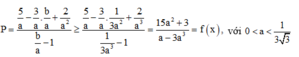
Xét hàm số:
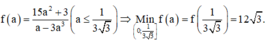
Chọn D.
ND
4
1 tháng 1 2017
(Câu trả lời của alibaba nguyễn đúng mà hài!!!)
Sơ đồ Horner hoạt động như sau:
| 1 | 0 | a | b | c | |
| 3 | 1 | 3 | a+9 | 3a+b+27 | 9a+3b+c+27 |
| 3 | 1 | 6 | a+27 | 6a+b+108 | 27a+6b+c+351 |
| 3 | ... | ... | ... | ... | ... |
- Kẻ bảng, trên dòng đầu tiên ghi các hệ số của đa thức đầu tiên, ở đây là \(1,0,a,b,c\).
- Theo định lí Bezout thì đa thức sẽ có nghiệm bội 3 là số 3, do đó chừa một cột bên tay trái ghi nghiệm (là số 3).
- Hạ hệ số (là 1) xuống, thực hiện quy tắc "nhân ngang cộng chéo" (nhân từ nghiệm qua rồi cộng chéo lên).
- VD: 3 nhân 1 cộng 0 là 3, viết 3. 3 nhân 3 cộng a là a+9, viết a+9. 3 nhân (a+9) cộng b là 3a+b+27, viết 3a+b+27...
- Để 3 là nghiệm của đa thức thì hệ số cuối cùng là 0, tức là \(9a+3b+c+27=0\).
- Tự làm tiếp, ra thêm 2 cái phương trình nữa...
26 tháng 12 2021
b: \(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow n\in\left\{0;-1;1\right\}\)
NN
1
7 tháng 2 2021
- Để hai đa thức trên chia cho nhau hết thì :\(\left\{{}\begin{matrix}7a-4=0\\b-2\left(1-3a\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}7a=4\\6a+b=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{4}{7}\\b=-\dfrac{10}{7}\end{matrix}\right.\)
Vậy ...