Cho hình chóp S.ABC có SA vuông góc (ABC), đáy là ΔABC vuông tại B, AB=a, \(BC=a\sqrt{3}\), \(SA=\dfrac{a\sqrt{6}}{2}\). Tính góc((SAC);(SBC))
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 5 2023
1:
a: BC vuông góc BA
BC vuông góc SA
=>BC vuông góc (SAB)
b: Kẻ BK vuông góc AC, BH vuông góc SK
=>BH=d(B;(SAC))
\(AC=\sqrt{BA^2+BC^2}=5a\)
AK=(4a)^2/5a=3,2a
BK=4a*3a/5a=2,4a
\(SB=\sqrt{2a^2+16a^2}=3a\sqrt{2}\)
SK=căn 2a^2+10,24a^2=a*3căn 34/5
BK=2,4a
SK^2+BK^2=SB^2
nên ΔSKB vuông tại K
=>K trùng với H
=>d(B;(SAC))=BK=2,4a
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 4 2021
1.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AB\\AD\perp AB\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SAD\right)\)
\(\Rightarrow\widehat{SBA}\) là góc giữa SB và (SAD)
\(tan\widehat{SBA}=\dfrac{SA}{AB}=\sqrt{3}\Rightarrow\widehat{SBA}=60^0\)
2.
\(SA\perp\left(ABC\right)\Rightarrow\left\{{}\begin{matrix}SA\perp AB\\SA\perp AC\end{matrix}\right.\) \(\Rightarrow\) các tam giác SAB và SAC vuông
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\BC\perp AB\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp SB\)
\(\Rightarrow\) Tam giác SBC vuông
Vậy tứ diện có 4 mặt đều là tam giác vuông (ABC hiển nhiên vuông theo giả thiết)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 4 2021
3.
a.
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\BC\perp AC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAC\right)\)
b.
Gọi M là trung điểm BC \(\Rightarrow IM||AC\)
\(\Rightarrow AC||\left(SIM\right)\Rightarrow d\left(AC;SI\right)=d\left(AC;\left(SIM\right)\right)=d\left(A;\left(SIM\right)\right)\)
Qua A kẻ đường thẳng song song BC cắt IM kéo dài tại K
\(\Rightarrow IM\perp AK\Rightarrow IM\perp\left(SAK\right)\)
Trong mp (SAK), kẻ AH vuông góc SK
\(\Rightarrow AH\perp\left(SIM\right)\Rightarrow AH=d\left(A;\left(SIM\right)\right)\)
\(AK=CM=\dfrac{b}{2}\)
\(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AK^2}\Rightarrow AH=\dfrac{SA.AK}{\sqrt{SA^2+AK^2}}=\dfrac{\dfrac{h.b}{2}}{\sqrt{h^2+\dfrac{b^2}{4}}}=\dfrac{bh}{\sqrt{b^2+4h^2}}\)
M
10 tháng 5 2021
Tự vẽ hình nhé:
a, Ta có: \(BC\perp AB\) (\(\Delta ABC\) vuông tại \(B\))
\(SA\perp BC\left(SA\perp\Delta ABC;BC\subset\left(ABC\right)\right)\)
\(AB\cap SA=\left\{A\right\}\)
\(AB,SA\subset\left(SAB\right)\)
\(\Rightarrow BC\perp\left(SAB\right)\)
b, Ta có \(BC\perp\left(SAB\right)\left(cmt\right)\)
mà \(SA\subset\left(SAB\right)\)
\(\Rightarrow BC\perp SA\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 4 2022
\(SA\perp\left(ABC\right)\Rightarrow AB\) là hình chiếu vuông góc của SB lên (ABC)
\(\Rightarrow\widehat{SBA}\) là góc giữa SB và (ABC)
\(AB=AC\sqrt{2}=a\sqrt{2}\)
\(tan\widehat{SBA}=\dfrac{SA}{AB}=\sqrt{\dfrac{3}{2}}\Rightarrow\widehat{SBA}\approx50^046'\)
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AC\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAC\right)\)
\(\Rightarrow SC\) là hình chiếu vuông góc của SB lên (SAC)
\(\Rightarrow\widehat{BSC}\) là góc giữa SB và (SAC)
\(SB=\sqrt{SA^2+AB^2}=a\sqrt{5}\) ; \(BC=AC=a\)
\(sin\widehat{BSC}=\dfrac{BC}{SB}=\dfrac{1}{\sqrt{5}}\Rightarrow\widehat{BSC}\approx26^034'\)
b.
Theo cmt, \(BC\perp\left(SAC\right)\)
Mà \(BC=\left(SBC\right)\cap\left(ABC\right)\)
\(\Rightarrow\widehat{SCA}\) là góc giữa (SBC) và (ABC)
\(tan\widehat{SCA}=\dfrac{SA}{AC}=\sqrt{3}\Rightarrow\widehat{SCA}=60^0\)
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\\SA\in\left(SAC\right)\end{matrix}\right.\) \(\Rightarrow\left(SAC\right)\perp\left(ABC\right)\)
\(\Rightarrow\) Góc giữa (SAC) và (ABC) là 90 độ
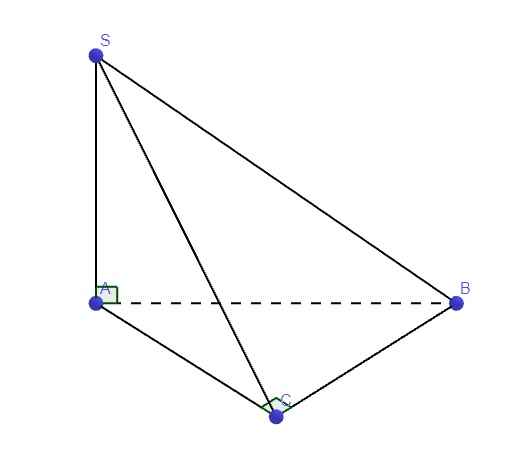
Trong mp (SAC), từ A kẻ \(AD\perp SC\) (D thuộc SC) (1)
Trong mp (ABC), qua A kẻ đường thẳng vuông góc AC cắt BC kéo dài tại E
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp AE\\AE\perp AC\end{matrix}\right.\) \(\Rightarrow AE\perp\left(SAC\right)\Rightarrow\left\{{}\begin{matrix}AE\perp AE\\AE\perp SC\left(2\right)\end{matrix}\right.\)
(1);(2) \(\Rightarrow SC\perp\left(ADE\right)\)
Mà \(SC=\left(SAC\right)\cap\left(SBC\right)\Rightarrow\widehat{ADE}\) là góc giữa (SAC) và (SBC)
\(AC=\sqrt{AB^2+BC^2}=2a\)
Hệ thức lượng: \(\dfrac{1}{AD^2}=\dfrac{1}{SA^2}+\dfrac{1}{AC^2}\Rightarrow AD=\dfrac{2a\sqrt{33}}{11}\)
\(\dfrac{1}{AB^2}=\dfrac{1}{AC^2}+\dfrac{1}{AE^2}\Rightarrow AE=\dfrac{AB.AC}{\sqrt{AC^2-AB^2}}=\dfrac{2a\sqrt{3}}{3}\)
\(\Rightarrow tan\widehat{ADE}=\dfrac{AE}{AD}=...\)