Một hộp có 20 lá thăm có kích thước giống nhau được đánh số từ 1 đến 20, hai lá
thăm khác nhau được đánh số khác nhau. Lấy ngẫu nhiên một lá thăm từ trong hộp. Xác suất của biến cố “Số được ghi trên lá thăm được rút ra là số có hai chữ số” là:
A. 9/20
B. 1/2
C. 11/20
D. 11
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì trong hộp có 10 là phiếu khác nhau từ 1 đến 10 nên xác suất ra 1 là thăm là như nhau.
b) Biến cố A có khả năng xảy ra là \(\frac{1}{{10}}\) do có 10 phiếu nên xác suất lấy được lá số 9 với các lá khác là như nhau.
c) Vì tất cả các lá phiếu là từ 1 đến 10 mà các số đều nhỏ hơn 11 nên biến cố B là biến cố chắc chắn.

Vì 5 quả bóng có kích thước và khối lượng giống nhau nên 5 kết quả của phép thử có khả năng xảy ra bằng nhau.
- Biến cố \(A\) xảy ra khi ta lấy được quả bóng có số 5 hoặc 13 nên có 2 kết quả thuận lợi cho \(A\). Xác suất của biến có \(A\) là:
\(P\left( A \right) = \frac{2}{5}\).
- Vì không có quả bóng nào đánh số chia hết cho 3 nên số kết quả thuận lợi của biến cố \(B\) là 0. Xác suất của biến cố \(B\) là
\(P\left( B \right) = \frac{0}{5} = 0\).
- Vì cả 5 quả bóng đều đánh số lớn hơn 4 nên số kết quả thuận lợi của biến cố \(C\) là 5. Xác suất của biến cố \(C\) là
\(P\left( C \right) = \frac{5}{5} = 1\).

Không gian mẫu là số sách lấy tùy ý 2 viên từ hộp chứa 12 viên bi.
Suy ra số phần tử của không gian mẫu là ![]() .
.
Gọi A là biến cố 2 viên bi được lấy vừa khác màu vừa khác số .
● Số cách lấy 2 viên bi gồm: 1 bi xanh và 1 bi đỏ là 4.4=16 cách (do số bi đỏ ít hơn nên ta lấy trước, có 4 cách lấy bi đỏ. Tiếp tục lấy bi xanh nhưng không lấy viên trùng với số của bi đỏ nên có 4 cách lấy bi xanh).
● Số cách lấy 2 viên bi gồm: 1 bi xanh và 1 bi vàng là 3.4=12cách.
● Số cách lấy 2 viên bi gồm: 1 bi đỏ và 1 bi vàng là 3.3=9 cách.
Suy ra số phần tử của biến cố A là 16+12+9=37.
Vậy xác suất cần tính 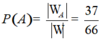 .
.
Chọn B.

a: \(\Omega=\left\{1;2;3;...;20\right\}\)
\(A=\left\{2;3;5;7;11;13;17;19\right\}\)
=>n(A)=8
=>P(A)=8/20=2/5
b: B={1;4;9;16}
=>n(B)=4
=>P(B)=4/20=1/5

Đáp án B
Lấy ngẫu nhiên 1 quả cầu trong 9 quả cầu có
![]()
Gọi A là biến cố “ lấy được quả cầu được đánh số là chẳn”
Trong 9 quả cầu đánh số, có các số chẵn là 2; 4; 6; 8
suy ra n(A) = 4
Vậy P ( A ) = 4 9

Đáp án B
Lấy ngẫu nhiên 1 quả cầu trong 9 quả cầu có C 9 1 cách ⇒ n Ω = 9
Gọi A là biến cố “ lấy được quả cầu được đánh số là chẳn”
Trong 9 quả cầu đánh số, có các số chẵn là 2 ; 4 ; 6 ; 8 suy ra n A = 4. Vậy P A = 4 9

Do các tấm thẻ giống nhau, nên lấy 3 tấm từ 10 tấm không quan tâm thứ tự có \(C_{10}^3 = 120\)cách, suy ra \(n\left( \Omega \right) = 120\)
Gọi A là biến cố “Tích các số ghi trên ba thẻ đó là số chẵn”
Để tích các số trên thẻ là số chẵn thì ít nhất có 1 thẻ là số chẵn
Để chọn ra 3 thẻ thuận lợi cho biến cố A ta có 3 khả năng
+) Khả năng 1: 3 thẻ chọn ra có 1 thẻ có số chẵn và 2 thẻ có số lẻ có \(5.C_5^2 = 50\) khả năng
+) Khả năng 2: 3 thẻ chọn ra có 2 thẻ có số chẵn và 1 thẻ có số lẻ có \(C_5^2.5 = 50\) khả năng
+) Khả năng 3: 3 thẻ chọn ra có đều là có số chắn có \(C_5^3 = 10\) khả năng
Suy ra \(n\left( A \right) = 50 + 50 + 10 = 110\)
Vậy xác suất của biến cố A là: \(P(A) = \frac{{110}}{{120}} = \frac{{11}}{{12}}\)

Có 6 cách chọn bi xanh.
Với mỗi cách chọn bi xanh có 6 cách chọn bi vàng để khác số.
Với mỗi cách chọn đó ta lại có 6 cách chọn bi đỏ để khác số với 2 quả vừa chọn.
Xác suất cần tìm là: \(\dfrac{6^3}{C_{21}^3}=\dfrac{108}{665}\).
Chọn B