Cho tam giác ABC ( AB < AC). Vẽ đường cao AH. Kẻ HE vuông góc với AB và HF vuông góc với AC ( E thuộc AB, F thuộc AC)
a) TG AEH dd TG AHB
b) AE.AB=AH^2 VÀ AE.AB = AF.AC
c) TG AFE dd TG ABC
d) MB.MC = ME.MF ( Biết đường thẳng EF cắt đường thẳng BC tại M )
cứu mik phần d vs mn ơiiiiii
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

30 tháng 8 2021
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH=\dfrac{60}{13}\left(cm\right)\)
b: Xét ΔABH vuông tại H có HE là đường cao ứng với cạnh huyền AB
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔACH vuông tại H có HF là đường cao ứng với cạnh huyền AC
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)

CM
4 tháng 1 2019
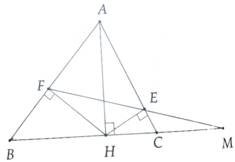
a, Ta có: ∆AEF ~ ∆MCE (c.g.c)
=> A F E ^ = A C B ^
b, Ta có: ∆MFB ~ ∆MCE (g.g)
=> ME.MF = MB.MC
a: Xét ΔAEH vuông tại E và ΔAHB vuông tại H có
góc EAH chung
=> ΔAEH đồng dạng với ΔAHB
b: ΔAHB vuông tại H có HE vuông góc AB
nên AH^2=AE*AB
ΔAHC vuông tại H
mà HF là đường cao
nên AF*AC=AH^2=AE*AB
c: AE*AB=AF*AC
=>AE/AC=AF/AB
=> ΔAEF đồng dạng với ΔACB
d: Xét ΔMEB và ΔMCF có
góc MEB=góc MCF
góc M chung
=> ΔMEB đồng dạng với ΔMCF
=>ME/MC=MB/MF
=>ME*MF=MB*MC