Tìm a để M⋮N và M : N dư 3 biết M = (\(x^4\) - x + 6x2 + a - x3) và N=(x2 -x+5)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 13:
1: \(A=-x^2+4x+3\)
\(=-\left(x^2-4x-3\right)=-\left(x^2-4x+4-7\right)\)
\(=-\left(x-2\right)^2+7\le7\)
Dấu '=' xảy ra khi x=2
2: \(B=-\left(x^2-6x+11\right)\)
\(=-\left(x-3\right)^2-2\le-2\)
Dấu '=' xảy ra khi x=3

Bài 12:
1) A = x2 - 6x + 11
= (x2 - 6x + 9) + 2
= (x - 3)2 + 2
Ta có: (x - 3)2 ≥ 0 ∀ x
Dấu ''='' xảy ra khi x - 3 = 0 ⇔ x = 3
Do đó: (x - 3)2 + 2 ≥ 2
Hay A ≥ 2
Dấu ''='' xảy ra khi x = 3
Vậy Min A = 2 tại x = 3
2) B = x2 - 20x + 101
= (x2 - 20x + 100) + 1
= (x - 10)2 + 1
Ta có: (x - 10)2 ≥ 0 ∀ x
Dấu ''='' xảy ra khi x - 10 = 0 ⇔ x = 10
Do đó: (x - 10)2 + 1 ≥ 1
Hay B ≥ 1
Dấu ''='' xảy ra khi x = 10
Vậy Min B = 1 tại x = 10
Cho A( x ) = x3 + mx + n ( n ; m thuộc Z ). Tìm m và n biết A : ( x - 1 ) dư 4 và A : ( x + 1 ) dư 6

cách 2 nếu chưa học bezout
x^3 +mx+n x-1 x^2+x+(m+1) x^3-x^2 - x^2+mx+n x^2-x - (m+1)x+n (m+1)x-(m+1) - n+m+1
Mà \(A\left(x\right):\left(x-1\right)\)dư 4\(\Rightarrow m+n+1=4\)
\(\Rightarrow m+n=3\left(1\right)\)
x^3 +mx+n x+1 x^2-x+(m+1) x^3+x^2 - -x^2+mx+n -x^2-x - (m+1)x+n (m+1)x+(m+1) - n-m-1
Mà \(A\left(x\right):\left(x+1\right)\)dư 6\(\Rightarrow n-m-1=6\)
\(\Rightarrow n-m=7\left(2\right)\)
Từ \(\left(1\right)\)và \(\left(2\right)\Rightarrow\hept{\begin{cases}n+m=3\\n-m=7\end{cases}\Rightarrow\hept{\begin{cases}n=5\\m=-2\end{cases}}}\)
Vậy n=5 và m=-2
Áp dụng định lý Bezout ta có:
\(A\left(x\right)\)chia x-1 dư 4 \(\Rightarrow A\left(1\right)=4\)
\(\Rightarrow1+m+n=4\)
\(\Rightarrow m+n=3\left(1\right)\)
\(A\left(x\right)\)chia x+1 dư 6 \(\Rightarrow A\left(-1\right)=6\)
\(\Rightarrow-1-m+n=6\)
\(\Rightarrow-m+n=7\left(2\right)\)
Từ \(\left(1\right)\)và \(\left(2\right)\Rightarrow\hept{\begin{cases}m+n=3\\-m+n=7\end{cases}\Rightarrow}\hept{\begin{cases}n=5\\m=-2\end{cases}}\)
Vậy n=5 và m=-2

Chọn B
Vì ba nghiêm phân biệt x 1 , x 2 , x 3 lập thành một cấp số cộng nên ta đặt : x 1 = x 0 + d , x 2 = x 0 , x 3 = x 0 + d ( d ≠ 0 )
Theo giả thuyết Ta có: x3+3x2 – (24+m)x – 26- n= (x – x1)(x-x2)(x-x3)
=(x-xo+d)(x-xo)(x-xo-d)= x3 – 3xox2+ (3xo2-d2)x-xo3+ xod2 với mọi x

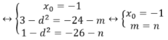
Vậy với m=n thì ba nghiệm phân biệt của phương trình lập thành một cấp số cộng

Để \(f\left(x\right):\left(x-1\right)R4\) thì \(x^3+mx+n=\left(x-1\right)\cdot a\left(x\right)+4\)
Thay \(x=1\Leftrightarrow m+n=4\left(1\right)\)
Để \(f\left(x\right):\left(x+1\right)R6\) thì \(x^3+mx+n=\left(x+1\right)\cdot b\left(x\right)+6\)
Thay \(x=-1\Leftrightarrow n-m-1=6\Leftrightarrow n-m=7\left(2\right)\)
Từ \(\left(1\right)\left(2\right)\Leftrightarrow\left\{{}\begin{matrix}m=\left(4-7\right):2=-\dfrac{3}{2}\\n=7+\left(-\dfrac{3}{2}\right)=\dfrac{11}{2}\end{matrix}\right.\)
Theo định lý Bơ du ta có:
Số dư của f(x) cho x-1 là \(f\left(1\right)\)
\(\Rightarrow f\left(1\right)=4\Rightarrow1+m+n=4\Leftrightarrow m+n=3\left(1\right)\)
Số dư của f(x) cho x+1 là \(f\left(-1\right)\)
\(\Rightarrow f\left(-1\right)=6\Rightarrow-1-m+n=6\Leftrightarrow-m+n=7\left(2\right)\)
Từ (1) và (2) ta có:
\(\left\{{}\begin{matrix}m=-2\\n=5\end{matrix}\right.\)
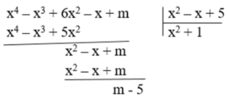

\(\dfrac{M}{N}=\dfrac{x^4-x^3+6x^2-x+a}{x^2-x+5}\)
\(=\dfrac{x^4-x^3+5x^2+x^2-x+5+a-5}{x^2-x+5}\)
\(=x^2+1+\dfrac{a-5}{x^2-x+5}\)
Để M chiahết cho N thì a-5=0
=>a=5
Để M chia N dư 3 thì a-5=3
=>a=8