Tính tổng S = \(\dfrac{1}{2}\) + \(\dfrac{2}{4}\) + \(\dfrac{3}{8}\) + \(\dfrac{4}{16}\) + ... + \(\dfrac{10}{2^{10}}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tìm y:
-y:1/2-5/2=4+1/2
-y:1/2 = 4+1/2+5/2
-y:1/2 = 7
-y = 7.2
y = -14
Vậy y = -14

\(\dfrac{3}{16}\) - (\(x\) - \(\dfrac{5}{4}\)) - ( \(\dfrac{3}{4}\) - \(\dfrac{7}{8}\) - 1) = 2\(\dfrac{1}{2}\)
\(\dfrac{3}{16}\) - \(x\) + \(\dfrac{5}{4}\) - \(\dfrac{3}{4}\) + \(\dfrac{7}{8}\) + 1 = \(\dfrac{5}{2}\)
\(\dfrac{3}{16}\) - \(x\) + ( \(\dfrac{5}{4}\) - \(\dfrac{3}{4}\)) + (\(\dfrac{7}{8}\) + 1) = \(\dfrac{5}{2}\)
\(\dfrac{3}{16}\) - \(x\) + \(\dfrac{1}{2}\) + \(\dfrac{15}{8}\) = \(\dfrac{5}{2}\)
( \(\dfrac{3}{16}\) + \(\dfrac{1}{2}\) + \(\dfrac{15}{8}\)) - \(x\) = \(\dfrac{5}{2}\)
\(\dfrac{41}{16}\) - \(x\) = \(\dfrac{5}{2}\)
\(x\) = \(\dfrac{41}{16}\) - \(\dfrac{5}{2}\)
\(x\) = \(\dfrac{1}{16}\)
2, \(\dfrac{1}{2}\).( \(\dfrac{1}{6}\) - \(\dfrac{9}{10}\)) = \(\dfrac{1}{5}\) - \(x\) + ( \(\dfrac{1}{15}\) - \(\dfrac{-1}{5}\))
\(\dfrac{1}{2}\).(-\(\dfrac{11}{15}\)) = \(\dfrac{1}{5}\) - \(x\) + \(\dfrac{1}{15}\) + \(\dfrac{1}{5}\)
- \(\dfrac{11}{30}\) = ( \(\dfrac{1}{5}\)+ \(\dfrac{1}{5}\)+ \(\dfrac{1}{15}\)) - \(x\)
- \(\dfrac{11}{30}\) = \(\dfrac{7}{15}\) - \(x\)
\(x\) = \(\dfrac{7}{15}\) + \(\dfrac{11}{30}\)
\(x\) = \(\dfrac{5}{6}\)

a: \(=\dfrac{14-2+9}{32}\cdot\dfrac{4}{5}=\dfrac{21}{5}\cdot\dfrac{1}{8}=\dfrac{21}{40}\)
b: \(=10+\dfrac{2}{9}+2+\dfrac{3}{5}+6+\dfrac{2}{9}=18+\dfrac{47}{45}=\dfrac{857}{45}\)
c: \(=\dfrac{3}{10}-\dfrac{12}{5}+\dfrac{1}{10}=\dfrac{4}{10}-\dfrac{12}{5}=\dfrac{2}{5}-\dfrac{12}{5}=-2\)
d: \(=\dfrac{-25}{30}\left(\dfrac{37}{44}+\dfrac{13}{44}-\dfrac{6}{44}\right)=\dfrac{-25}{30}\cdot1=-\dfrac{5}{6}\)

`@` `\text {Ans}`
`\downarrow`
`1,`
`3/16 - (x - 5/4) - (3/4 + (-7)/8 - 1) = 2 1/2`
`=> 3/16 - x + 5/4 - (-1/8 - 1) = 2 1/2`
`=> 3/16 - x + 5/4 - (-9/8) = 2 1/2`
`=> 3/16 - x + 19/8 = 2 1/2`
`=> 3/16 - x = 2 1/2 - 19/8`
`=> 3/16 - x =1/8`
`=> x = 3/16 - 1/8`
`=> x = 1/16`
Vậy, `x = 1/16`
`2,`
`1/2* (1/6 - 9/10) = 1/5 - x + (1/15 - (-1)/5)`
`=> 1/2 * (-11/15) = 1/5 - x + 4/15`
`=> -11/30 = x + 1/5 - 4/15`
`=> x + (-1/15) = -11/30`
`=> x = -11/30 + 1/15`
`=> x = -3/10`
Vậy, `x = -3/10.`
 b)
b) 
 d)
d) 
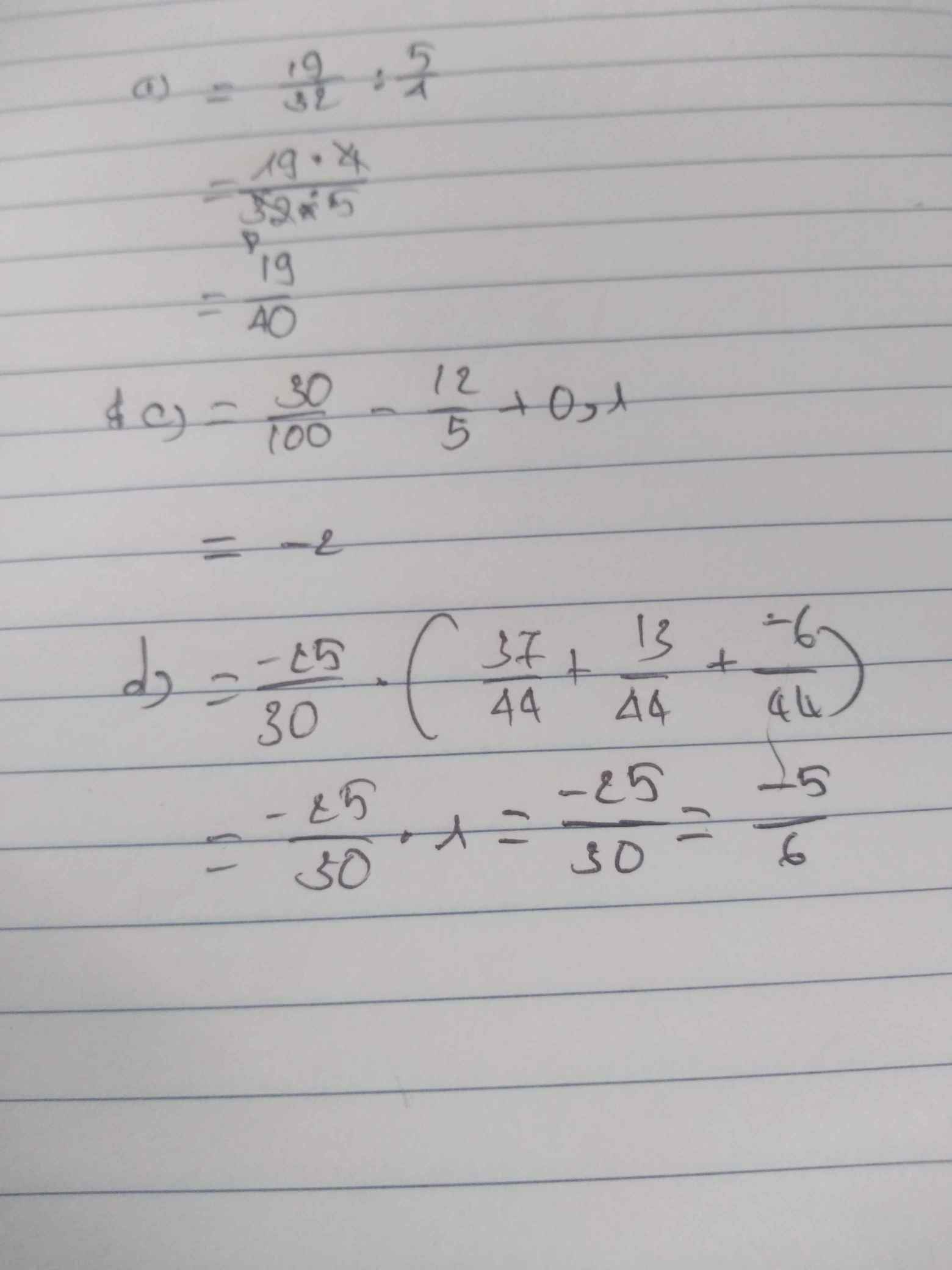
Ta có S = \(\dfrac{1}{2}+\dfrac{2}{4}+\dfrac{3}{8}+\dfrac{4}{16}+...+\dfrac{10}{2^{10}}\)
= \(\dfrac{1}{2}+\dfrac{2}{2^2}+\dfrac{3}{2^3}+\dfrac{4}{2^4}+...+\dfrac{10}{2^{10}}\)
2S = 1 + \(\dfrac{2}{2}+\dfrac{3}{2^2}+\dfrac{4}{2^3}+...+\dfrac{10}{2^9}\)
2S - S = ( 1 + \(\dfrac{2}{2}+\dfrac{3}{2^2}+\dfrac{4}{2^3}+...+\dfrac{10}{2^9}\)) - ( \(\dfrac{1}{2}+\dfrac{2}{2^2}+\dfrac{3}{2^3}+\dfrac{4}{2^4}+...+\dfrac{10}{2^{10}}\))
S = 1 + \(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^9}-\dfrac{10}{2^{10}}\)
Đặt A = 1 + \(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^9}\)
2A = 2 + 1 + \(\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^8}\)
2A - A = ( 2 + 1 + \(\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^8}\)) - ( 1 + \(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^9}\))
A = 2 - \(\dfrac{1}{2^9}\)
⇒ S = 2 - \(\dfrac{1}{2^9}\) - \(\dfrac{10}{2^{10}}\) = \(\dfrac{2^{11}}{2^{10}}-\dfrac{2}{2^{10}}-\dfrac{10}{2^{10}}=\dfrac{2^2\left(2^9-3\right)}{2^{10}}=\dfrac{2^9-3}{2^8}\)
Vậy S = \(\dfrac{2^9-3}{2^8}\)