tìm nghiệm của đa thức 6x2+13x-8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cho `P(x)=0`
`=>6x^2-7x-3=0`
`=>6x^2+2x-9x-3=0`
`=>2x(3x+1)-3(3x+1)=0`
`=>(3x+1)(2x-3)=0`
`=>` $\left[\begin{matrix} 3x+1=0\\ 2x-3=0\end{matrix}\right.$
`=>` $\left[\begin{matrix} x=\dfrac{-1}{3}\\ x=\dfrac{3}{2}\end{matrix}\right.$
Vậy đa thức có nghiệm `x = [-1]/3` hoặc `x=3/2`
cho P(x) = 0
\(6x^2-7x-3=0\)
\(\Leftrightarrow6x^2+2x-9x-3=0\)
\(\Leftrightarrow2x\left(3x+1\right)-3\left(3x+1\right)=0\)
\(\Leftrightarrow\left(2x-3\right)\left(3x+1\right)=0\)
\(=>\left[{}\begin{matrix}2x=3\\3x=-1\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-\dfrac{1}{3}\end{matrix}\right.\)

\(\hept{\begin{cases}x_1=\frac{5}{2}\\x_2=\frac{7}{3}\end{cases}}\)

P(x) = \(-x^4-5x^3-6x^2+5x-1\)
Q(x) = \(x^4+5x^3+6x^2-2x+3\)
M(x) = P(x) + Q(x)
\(-x^4-5x^3-6x^2+5x-1\)
+
\(x^4+5x^3+6x^2-2x+3\)
------------------------------------
\(3x+2\)
Vậy : M(x) = 3x + 2
Nghiệm của M(x) : 3x + 2 = 0
3x = -2
x = \(-\dfrac{2}{3}\)
a) \(P\left(x\right)=x^4-5x^3-1-6x^2+5x-2x^4\)
\(P\left(x\right)=\left(x^4-2x^4\right)-5x^3-1-6x^2+5x\)
\(P\left(x\right)=-x^4-5x^3-1-6x^2+5x\)
\(P\left(x\right)=-x^4-5x^3-6x^2+5x-1\)
\(Q\left(x\right)=3x^4+6x^2+5x^3+3-2x^4-2x\)
\(Q\left(x\right)=\left(3x^4-2x^4\right)+6x^2+5x^3+3-2x\)
\(Q\left(x\right)=x^4+6x^2+5x^3+3-2x\)
\(Q\left(x\right)=x^4+5x^3+6x^2-2x+3\)
b) Ta có \(M\left(x\right)=P\left(x\right)+Q\left(x\right)\)
\(\begin{matrix}\Rightarrow P\left(x\right)=-x^4-5x^3-6x^2+5x-1\\Q\left(x\right)=x^4+5x^3+6x^2-2x+3\\\overline{P\left(x\right)+Q\left(x\right)=0+0+0+3x+2}\end{matrix}\)
Vậy \(M\left(x\right)=3x+2\)
Cho \(M\left(x\right)=0\)
hay \(3x+2=0\)
\(3x\) \(=0-2\)
\(3x\) \(=-2\)
\(x\) \(=-2:3\)
\(x\) \(=\dfrac{-2}{3}\)
Vậy \(x=\dfrac{-2}{3}\) là nghiệm của đa thức \(M\left(x\right)\)

Đặt \(6x^2+2x+2=0\)
\(\text{Δ}=2^2-4\cdot6\cdot2=4-48=-44< 0\)
Do đó: Phương trình vô nghiệm

3x2 -13x +4 = 0
<=>3x2 -x -12x +4 = 0
<=> x( 3x-1) -4 (3x-1) = 0
<=> (x-4)(3x-1)=0
Vậy x =4 hoặc x =1/3

x4 - 13x2 + 36 = 0
x4 - 13x2 = -36
x2.(x2 - 13) = -36
Ta có: Các ước chính phương của -36 là 1 ; 4 ; 9 ; 36 => x thuộc {-6 ; -3 ; -2; -1 ; 1 ; 2; 3; 6}
Vậy x thuộc {-3 ; -2 ; 2; 3}

Đặt D(x)=0
\(\Leftrightarrow2x^2-13x+15=0\)
\(\Leftrightarrow2x^2-3x-10x+15=0\)
=>(2x-3)(x-5)=0
=>x=3/2 hoặc x=5

a) P(x) = 5x5 - 4x2 + 7x + 15
Q(x) = 5x5 - 4x2 + 3x + 8
b) Có: P(x) - Q(x) = 4x + 7
P(x) - Q(x) = 0 <=> x = \(-\dfrac{-7}{4}\)
`a,```P(x) = 8x^5 +7x -6x^2 -3x^5 +2x^2+15`
`= (8x^5 -3x^5 ) +(-6x^2+2x^2) +7x+15`
`=5x^5 -4x^2 +7x+15`
`Q(x) =4x^5 +3x-2x^2 +x^5 -2x^2+8`
`=(4x^5+x^5) +(-2x^2 -2x^2)+3x+8`
`= 5x^5 - 4x^2 +3x+8`
`b, P(x) -Q(x)=(5x^5 -4x^2 +7x+15)-(5x^5 - 4x^2 +3x+8)`
`= 5x^5 -4x^2 +7x+15-5x^5 +4x^2 -3x-8`
`= (5x^5-5x^5)+(-4x^2+4x^2) +(7x-3x)+(15-8)`
`= 0 + 0 +4x + 7`
`=4x+7`
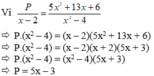
=> 6x2 - 3x + 16x - 8 =0 => 3x(2x - 1) + 8(2x - 1) =0 => (3x + 8)(2x - 1) =0 => 3x+8 =0 => x=-8/3 và 2x-1=0 => x=-1/2
\(6x^2+13x-8=0\)
\(\Leftrightarrow6x^2+16x-3x-8=0\)
\(\Leftrightarrow6x\left(x+\frac{8}{3}\right)-3\left(x+\frac{8}{3}\right)=0\)
\(\Leftrightarrow\left(x+\frac{8}{3}\right)\left(6x-3\right)=0\)
Ra phương trình tích rồi, bạn cho từng cái = 0 và giải ra tìm x nhé