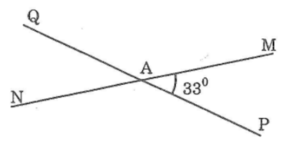
hai đường thẳng MN và PQ cắt nhau tại Atao thành góc MAP có số đo bằng 30
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vì góc NAQ và góc MAP là hai góc đối đỉnh
=> MAP = NAQ = 30 độ

Ta có:
∠NAQ và ∠PAM là hai góc đối đỉnh
Suy ra:∠NAQ = ∠MAP
mà ∠MAP = 33o nên ∠NAQ = 33o
Vậy góc NAQ = 33 độ
Hok tốt thấy đúng k cho mình nhé !

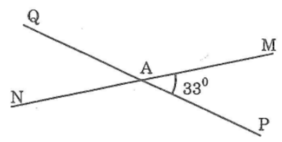
∠PAM và ∠MAQ là hai góc kề bù nên ∠PAM + ∠MAQ=180o
Suy ra: ∠MAQ = 180o-∠PAM =180o-33o=147o

Ta có:
∠NAQ và ∠PAM là hai góc đối đỉnh
Suy ra:∠NAQ = ∠PAM
mà ∠PAM = 33o nên ∠NAQ = 33o

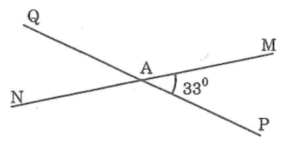
Các cặp góc kề bù là: ∠PAM và ∠MAQ; ∠PAM và ∠PAN ; ∠NAQ và ∠PAN ; ∠NAQ và ∠QAM

M N P Q A
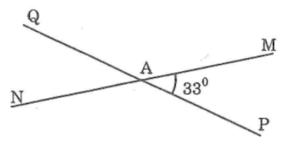
a) Vì góc MAP và NAQ là 2 góc đối đỉnh
=> MAP = NAQ = 42o
Vì MAP và MAQ là 2 góc kề bù
=> MAP + MAQ = 180o => MAQ = 180o - 42o = 138o
b) Các cặp góc đối đỉnh: MAP và NAQ ; MAQ và NAP

a) Ta có:
∠MAP= ∠NAQ (hai góc đối đỉnh)
⇒ ∠NAQ = 45o
⇒ ∠NAQ = 45o
b) Ta có:
∠MAP + ∠MAQ = 180o ( hai góc kề bù )
⇒ 45o + ∠MAQ = 180o
⇒ ∠MAQ = 180o − 45o = 135o
c) Các cặp góc đối đỉnh là:
∠MAP, ∠NAQ
∠NAP, ∠MAQ
d) Các cặp góc bù nhau là:
∠MAP, ∠NAP
∠MAP, ∠MAQ
∠NAQ, ∠NAP
∠NAQ, ∠MAQ
thiếu đầu bài rồi
thì chúng tạo thành 1 góc 30 độ hết
k nhá