cho tam giác abc có ab =4cm bc=5cm ac=7cm .sắp xếp các góc abc theo thứ tự từ lớn đến bé B.cho đoạn thẳng mn có độ dài bằng 6cm vẽ đường trung trực d của đoạn thẳng mn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H
4 tháng 5 2023
a, Ta có góc đối diện với cạnh nhỏ nhất là góc lớn nhất
mà \(AB< AC< BC\left(4< 6< 7\right)\)
\(\Rightarrow\widehat{C}< \widehat{B}< \widehat{A}\)
Sắp xếp : \(\widehat{C},\widehat{B},\widehat{A}\)
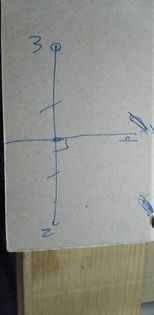
b, Cách vẽ đường trung trực
Bước 1 Xác định trung điểm của MN
Giả sử : I là trung điểm MN
Bước 2 Vẽ \(IM=\dfrac{1}{2}MN=\dfrac{1}{2}.5=2,5\left(cm\right)\)
Bước 3 vẽ đường thẳng vuông góc với MN đi qua I
Hình vẽ :
CM
14 tháng 1 2018
Đáp án là A
Ta có: AB = 4cm; MN = 5cm; EF = 3cm; PQ = 8cm; IK = 7cm
Do đó, các đoạn thẳng được sắp xếp theo thứ tự độ dài tăng dần là: EF, AB, MN, IK, PQ
H
6 tháng 5 2022
Cậu tự vẽ hình
a. Xét tg ABC có:
BC2= 102=100
AB2 + AC2= 62 + 82 = 36 + 64 = 100
=> BC2=AB2 + AC2
=> Tam giác ABC vuông tại A (định lý Py-ta-go đảo)
b. Xét △BKM và △CKD vuông tại K có:
MK chung
BK=KC (K là trung điểm BC)
=> △BKM = △CKD (2cgv)
=> BM=CM (2 cạnh tương ứng)
Xét △DMC vuông tại D và △AMB vuông tại A có:
MB=CM (cmt)
góc BMC chung
=> △DMC = △AMB (ch-gn)
=> AB=DC (2 cạnh tương ứng)
25 tháng 7 2021
Xét ΔABC có
\(\dfrac{AM}{AB}=\dfrac{AN}{AC}\left(=\dfrac{1}{4}\right)\)
Do đó: MN//BC(Định lí Ta lét đảo)
Xét ΔABC có MN//BC(cmt)
nên \(\dfrac{MN}{BC}=\dfrac{AM}{AB}\)(Hệ quả của Định lí Ta lét)
\(\Leftrightarrow MN=\dfrac{1}{4}\cdot8=2\left(cm\right)\)
31 tháng 7 2023
a: AD>AB>CD>BC
b: Độ dài đường gấp khúc là 7+5+6+12=30cm
c: Độ dài đường gấp khúc ABCD=30cm
AD=12cm
=>Độ dài đường gấp khúc ABCD lớn hơn AD
Sắp xếp các gốc theo thứ tự từ lớn đến bé:
Ta có: \(AC>BC>AB\)
\(\Rightarrow\widehat{B}>\widehat{A}>\widehat{C}\)