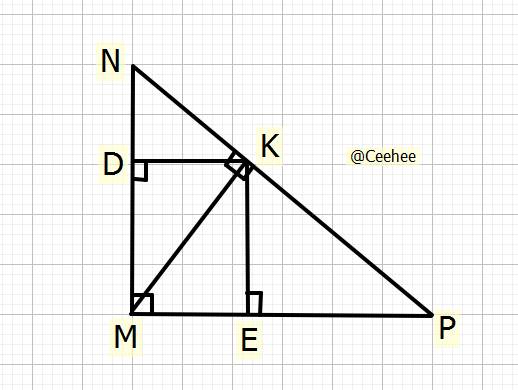
Cho tam giác MNP vuông tại M, đường cao MH. Gọi D và E lần lượt là hình chiếu của H trên MN, MP.
a) Tính DE biết MN=15cm, MP=20cm.
b) Chứng Minh \(\widehat{MDE=}\widehat{P}\)
c) Chứng minh MD.MN = MP.ME.
d) Tam giác MNP phải có thêm điều kiện gì để diện tích tứ giác MEHD bằng một nửa diện tích tam giác MNP.
Giải đầy đủ nha!!
Thanks!