cho 2 đường thẳng phân biệt không song song;không vuông góc a và b,điểm M không nằm trên 2 đường thẳng này.Qua M lần lượt vẽ đường thẳng c vuông góc với A tại b,cắt b tại Q và đường thẳng d vuông góc với b tại R, cắt a tại S.Chứng minh rằng đường thẳng qua M,vuông góc với SQ cũng đi qua giao điểm của a và b
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 2 2018
Đáp án C
2. Nếu 3 mặt phẳng đôi một cắt nhau theo 3 giao tuyến phân biệt thì 3 giao tuyến ấy hoặc đồng quy, hoặc đôi một song song với nhau
8. Cho 2 đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia
LH
20 tháng 5 2017
Mỗi câu sau đây là đúng hay sai ?
a) Có một và chỉ một đường thẳng đi qua hai điểm (phân biệt) cho trước
Đúng
b) Có đúng ba đường thẳng đi qua ba điểm (phân biệt) cho trước
Sai
c) Có đúng 6 đường thẳng đi qua bốn điểm (phân biệt) cho trước
Sai
d) Hai đường thẳng phân biệt thì song song với nhau
Sai
e) Hai đường thẳng không cắt nhau thì song song với nhau
Sai
f) Hai đường thẳng không song song thì cắt nhau
Sai
g) Hai đường thẳng không phân biệt thì trùng nhau
Đúng
h) Ba đường thẳng phân biệt, từng đôi một cắt nhau thì có đúng 3 giao điểm (phân biệt)
Sai
CM
6 tháng 4 2019
a) Đúng
b) Sai. Vì hai đường thẳng không cắt nhau có thể song song hoặc trùng nhau.
c) Đúng
d) Đúng
e) Đúng
f) Đúng
24 tháng 10 2021
Lấy bài ng khác thì ghi tham khảo vào chứ bạn :)
Đã vậy còn phải xem đúng đề k đã
Bạn cứ tiếp tục như vậy thì mỗi lần bạn đăng câu trl lên mình sẽ xóa hết nhé
CM
23 tháng 1 2019
Vì vai trò của m,n như nhau nên với mỗi n sẽ có 1 m tương ứng
Vậy có tất cả 4 bộ số thỏa mãn yêu cầu bài toán Chọn B
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
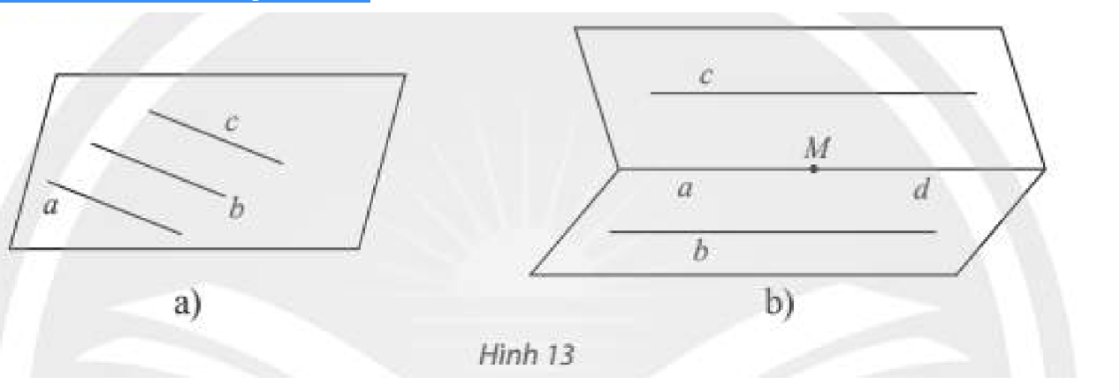
Ta có: \(d = mp\left( {a,c} \right) \cap mp\left( {M,b} \right) \Rightarrow M \in d\)
Lại có: \(M \in a\)
Mà qua \(M\) chỉ có một đường thẳng song song với đường thẳng \(b\) nên \(d \equiv a\).
Do đó \(a\parallel b\).
CM
15 tháng 6 2019
Hai đường thẳng song song là hai đường thẳng không có điểm chung
a. Đúng
b. sai (vì hai đường thẳng không cắt nhau có thể trùng nhau)
c. Đúng
d. Đúng
CM
19 tháng 12 2017
Đáp án B
Các cách xác định mặt phẳng đúng: 2; 4 ; 8
1. Đi qua 3 điểm phân biệt không thẳng hàng
3. Trong trường hợp 2 đường thẳng chéo nhau thì không thể xác định được mặt phẳng
5. Song song với 2 đường thẳng cắt nhau Có vô số mặt phẳng như vậy.
Phương pháp xác định mặt phẳng chỉ đúng khi mặt phẳng này đi qua 1 điểm cho trước
6. Song song với 2 đường thẳng chéo nhau Có vô số mặt phẳng như vậy
Phương pháp xác định mặt phẳng chỉ đúng khi mặt phẳng này đi qua 1 điểm cho trước
7. Đi qua 1 điểm và song song với một đường thẳng cho trước. Có vô số mặt phẳng như vậy