Kíu típ :__________(
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



A B C H D
a)Xét \(\Delta ABC\) vuông tại A có:
\(BC^2=AC^2+AB^2\)
\(BC^2=64+36\)
\(BC^2=100\)
BC=10cm
Xét \(\Delta ABC\) có: AD là phân giác của\(\widehat{BAC}\)
=> \(\dfrac{BD}{AB}=\dfrac{DC}{AC}=\dfrac{BD+DC}{AB+AC}=\dfrac{BC}{AB+AC}=\dfrac{10}{6+8}=\dfrac{5}{7}\)
=> \(\dfrac{BD}{AB}=\dfrac{5}{7}\Leftrightarrow\dfrac{BD}{6}=\dfrac{5}{7}\Rightarrow BD=\dfrac{5}{7}.6\approx4,3\) cm
b)
Xét \(\Delta HBA\) và \(\Delta ABC\) có:
\(\widehat{B}\) chung
\(\widehat{BHA}=\widehat{BAC}\left(=90^o\right)\)
=> \(\Delta HBA\sim\)\(\Delta ABC\) (g-g)
=> \(\dfrac{AH}{AC}=\dfrac{AB}{BC}\Leftrightarrow\dfrac{AH}{8}=\dfrac{6}{10}\Rightarrow AH=\dfrac{3}{5}.8=4,8cm\)
\(\dfrac{HB}{AB}=\dfrac{AB}{BC}\Leftrightarrow\dfrac{HB}{6}=\dfrac{6}{10}\Rightarrow HB=\dfrac{3}{5}.6=3,6cm\)
c) Có : \(\dfrac{HB}{AB}=\dfrac{AB}{BC}\) ( \(\Delta HBA\sim\)\(\Delta ABC\) )
=> \(AB^2=HB.BC\)

a,\(\dfrac{37}{12}-3=\dfrac{37}{12}-\dfrac{3}{1}=\dfrac{37}{12}-\dfrac{36}{12}=\dfrac{1}{12}\)
b,\(\dfrac{4}{5}x\dfrac{6}{7}=\dfrac{24}{35}\)
15237
+ 6542
----------
21779
b, 3444 l 28
64 l ------------
84 l 123
0

a: \(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=9\end{matrix}\right.\)






 Ai kíu tui đy
Ai kíu tui đy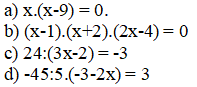




\(\dfrac{x+1}{99}+\dfrac{x+2}{98}+\dfrac{x+3}{97}+\dfrac{x+4}{96}=-4\)
⇔\(\dfrac{x+1}{99}+1+\dfrac{x+2}{98}+1+\dfrac{x+3}{97}+\dfrac{x+4}{96}=-4+1+1+1+1\)
⇔\(\dfrac{x+1}{99}+\dfrac{99}{99}+\dfrac{x+2}{98}+\dfrac{98}{98}+\dfrac{x+3}{97}+\dfrac{97}{97}+\dfrac{x+4}{96}+\dfrac{96}{96}=-4+4\)
⇔\(\dfrac{x+100}{99}+\dfrac{x+100}{98}+\dfrac{x+100}{97}+\dfrac{x+100}{96}=0\)
⇔\(\left(x+100\right)\left(\dfrac{1}{99}+\dfrac{1}{98}+\dfrac{1}{97}+\dfrac{1}{96}\right)=0\)
⇔\(x+100=0\left(\dfrac{1}{99}+\dfrac{1}{98}+\dfrac{1}{97}+\dfrac{1}{96}\ne0\right)\)
⇔\(x=-100\)
cíu được phần 1 thôi nhé
Bổ xung ý 2
\(\dfrac{1}{x}+\dfrac{y}{3}=\dfrac{5}{6}\\ \Rightarrow\dfrac{1}{x}=\dfrac{5}{6}-\dfrac{y}{3}\\ \Rightarrow\dfrac{1}{x}=\dfrac{5-2y}{6}\\ \Rightarrow x\cdot\left(5-2y\right)=6\)
`=>x;5-2y in Ư(6)={+-1;+-3;+-2;+-6}`
mà `5-2y` là số lẻ
nên `5-2y in {+-1;+-3}`
Ta có bảng sau :
Vậy `x;y in {(1;2);(3;1)}`