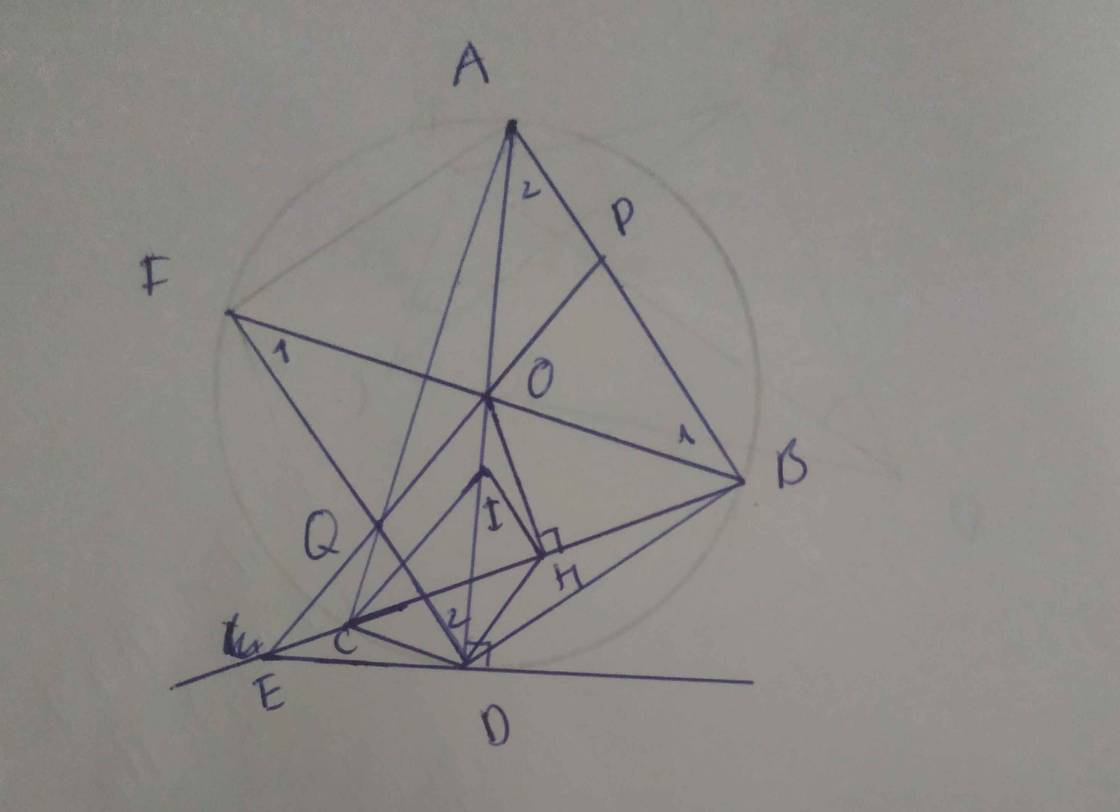
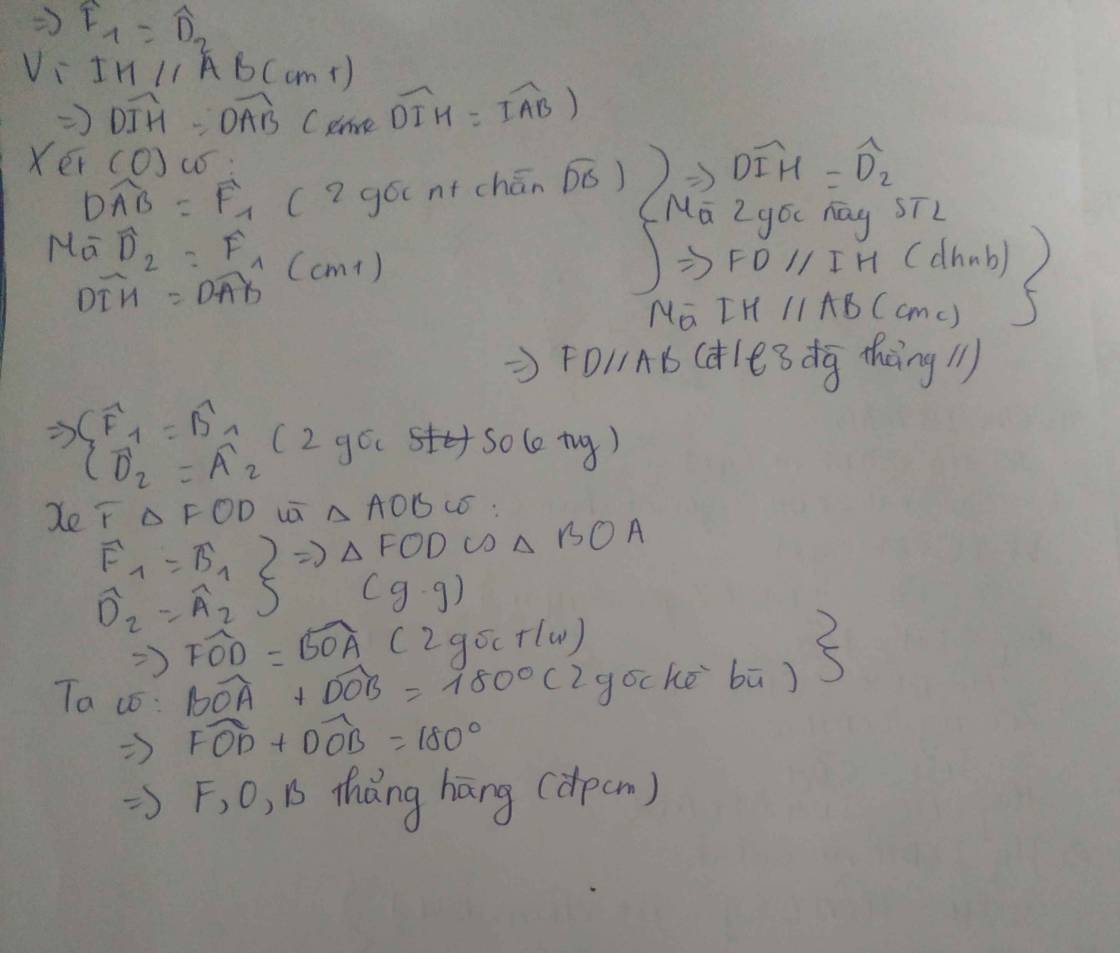Cho đường tròn (O;R) ngoại tiếp tam giác nhọn ABC (AC>AB). Kẻ đường kính AD của đường tròn (O). Tiếp tuyến tại D của đường tròn (O;R) cắt đường thẳng BC tại E. Kẻ OH vuông góc với BC tại H.
Có OHDE nội tiếp. Có ED^2=EC.EB.
Từ C kẻ đường thẳng song song với OE, đường này cắt AD tại I.
a) Chứng minh HI//AB
b) Đường thẳng OE cắt AB và AC lần lượt tại P và Q. Gọi F là giao điểm thứ hai của DQ với đường tròn (O;R). Chứng minh ba điểm B,O,F thẳng hàng.