Cho tam giác ABC có \(\widehat{B}+\widehat{C}=105\) và \(AB+AC\sqrt{2}=2BC\) . Tính góc B và góc C
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NM
6
A
15 tháng 3 2018
De cho gon dat ^BAC = A = 75°; ^ABC = B; ^ACB = C; BC = a; CA = b; AB = c
cosA = cos75° = cos(45° + 30°) = cos45°cos30° - sin45°sin30° = ( √6 - √2)/4
Theo gia thiet vs theo dinh ly hs cosin
{ c + b√2 = 2a (1)
{ a² = b² + c² - 2bc.cosA
<=>
{ 2b² + c² + 2√2bc = 4a²
{ 4b² + 4c² - 2(√6 - √2)bc = 4a²
Tru 2 pt cho nhau :
2b² + 3c² - 2√6bc = 0 <=> (√2b - √3c)² = 0 <=> √2b - √3c = 0
<=> √2sinB - √3sinC = 0 (theo dinh ly hs sin)
<=> sinC = √2.sinB/√3 (1)
Mat khac :
C = 105° - B <=> sinC = sin(105° - B) = sin105°cosB - cos105°sinB (2)
voi sin105° = sin75° = √(1 - cos²75°) = (2 + √3)/4 (3)
cos105° = - cos75° = (√2 - √6)/4 (4)
Thay (1); (3); (4) vao (2) rut gon ta co :
tanB = (3 + 2√3)/(√6 + √2) = (√6 + 3√2)/4
=> B; C
15 tháng 3 2018
Về phía ngoài của \(\Delta\)ABC vẽ \(\Delta\)ACD vuông cân tại C.
Trên nửa mặt phẳng bờ AD không chứa B và C vẽ \(\Delta\)ADE đều.
Dễ dàng tính được: \(\widehat{BAC}=180^0-\left(\widehat{ABC}+\widehat{ACB}\right)=180^0-105^0=75^0\)
Do \(\Delta\)ACD vuông cân tại C => \(\widehat{CAD}=45^0\); \(\Delta\)ADE đều => \(\widehat{DAE}=60^0\)
=> \(\widehat{ABC}+\widehat{CAD}+\widehat{DAE}=75^0+45^0+60^0=180^0\)
=> 3 điểm B;A;E là 3 điểm thẳng hàng => \(AB+AE=BE\)(1)
Xét \(\Delta\)ACD: \(\widehat{ACD}=90^0;AC=CD\)=> \(AD^2=AC^2+CD^2=2.AC^2\)(ĐL Pytago)
=> \(AD=\sqrt{2}.AC\). Mà \(\Delta\)ADE đều => AD=AE\(\Rightarrow AE=\sqrt{2}.AC\)(2)
Từ (1) và (2) => \(BE=AB+AC.\sqrt{2}\).
Lại có: \(AB+AC.\sqrt{2}=2BC\)=> \(BE=2.BC\)
Ta thấy: EA=ED; CA=CD => E và C thuộc đường trung trực của AD => EC\(\perp\)AD (3)
=> \(\widehat{AEC}=30^0\)hay \(\widehat{BEC}=30^0\)
Xét \(\Delta\)ECB có: \(\widehat{BEC}=30^0\); \(BE=2.BC\)=> \(\Delta\)ECB vuông tại C hay EC\(\perp\)BC (4)
Từ (3) và (4) => AD // BC => \(\widehat{BCA}=\widehat{CAD}\)(So le trong). Mà \(\widehat{CAD}=45^0\)\(\Rightarrow\widehat{BCA}=45^0.\)
Vậy \(\widehat{BCA}=45^0\).
.
AH
Akai Haruma
Giáo viên
30 tháng 8 2020
Trần Quốc Khanh: ừ ha. Mà định lý sin và cos thì nổi tiếng quá rồi. Cách chứng minh có thể tham khảo trên google =)))
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 8 2021
\(\dfrac{B}{C}=\dfrac{4}{3}\Rightarrow B=\dfrac{4C}{3}\)
\(B+C=180^0-A=105^0\Rightarrow C+\dfrac{4C}{3}=105^0\Rightarrow C=45^0\) \(\Rightarrow B=60^0\)
Kẻ đường cao AD ứng với BC (do 2 góc B và C đều nhọn nên D nằm giữa B và C)
Trong tam giác vuông ABD:
\(sinB=\dfrac{AD}{AB}\Rightarrow AD=AB.sinB=10,6.sin60^0\approx9,2\left(cm\right)\)
\(cosB=\dfrac{BD}{AB}\Rightarrow BD=AB.cosB=10,6.cos60^0=5,3\left(cm\right)\)
Trong tam giác vuông ACD:
\(tanC=\dfrac{AD}{CD}\Rightarrow CD=AD.tanC=9,2.tan45^0=9,2\left(cm\right)\)
\(sinC=\dfrac{AD}{AC}\Rightarrow AC=\dfrac{AD}{sinC}=\dfrac{9,2}{sin45^0}\approx13\left(cm\right)\)
\(BC=BD+CD=5,3+9,2=14,5\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}AD.BC=\dfrac{1}{2}.9,2.14,5=66,7\left(cm^2\right)\)
17 tháng 9 2023
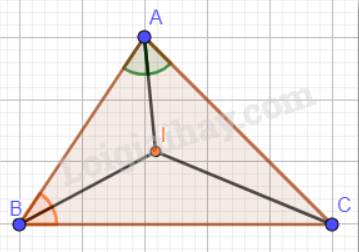
Ta có: I là giao điểm của hai đường phân giác góc A và góc B nên suy ra: CI là đường phân giác của góc C.
Vậy \(\widehat {ICA} = \widehat {ICB}\) ( tính chất tia phân giác của một góc).
Đáp án: A. \(\widehat {ICA} = \widehat {ICB}\).
25 tháng 9 2023
Tham khảo:
a) Áp dụng hệ quả của định lí cosin, ta có:
\(\begin{array}{l}\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}};\cos B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}}\\ \Rightarrow \left\{ \begin{array}{l}\cos A = \frac{{{{10}^2} + {{13}^2} - {8^2}}}{{2.10.13}} = \frac{{41}}{{52}} > 0;\\\cos B = \frac{{{8^2} + {{13}^2} - {{10}^2}}}{{2.8.13}} = \frac{{133}}{{208}} > 0\\\cos C = \frac{{{8^2} + {{10}^2} - {{13}^2}}}{{2.8.10}} = - \frac{1}{{32}} < 0\end{array} \right.\end{array}\)
\( \Rightarrow \widehat C \approx 91,{79^ \circ } > {90^ \circ }\), tam giác ABC có góc C tù.
b)
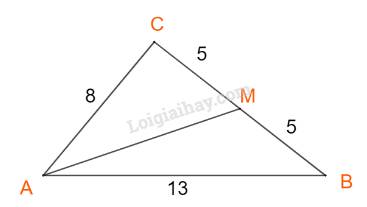
+) Áp dụng định lí cosin trong tam giác ACM, ta có:
\(\begin{array}{l}A{M^2} = A{C^2} + C{M^2} - 2.AC.CM.\cos C\\ \Leftrightarrow A{M^2} = {8^2} + {5^2} - 2.8.5.\left( { - \frac{1}{{32}}} \right) = 91,5\\ \Rightarrow AM \approx 9,57\end{array}\)
+) Ta có: \(p = \frac{{8 + 10 + 13}}{2} = 15,5\).
Áp dụng công thức heron, ta có: \(S = \sqrt {p(p - a)(p - b)(p - c)} = \sqrt {15,5.(15,5 - 8).(15,5 - 10).(15,5 - 13)} \approx 40\)
+) Áp dụng định lí sin, ta có:
\(\frac{c}{{\sin C}} = 2R \Rightarrow R = \frac{c}{{2\sin C}} = \frac{{13}}{{2.\sin 91,{{79}^ \circ }}} \approx 6,5\)
c)
Ta có: \(\widehat {BCD} = {180^ \circ } - 91,{79^ \circ } = 88,{21^ \circ }\); \(CD = AC = 8\)
Áp dụng định lí cosin trong tam giác BCD, ta có:
\(\begin{array}{l}B{D^2} = C{D^2} + C{B^2} - 2.CD.CB.\cos \widehat {BCD}\\ \Leftrightarrow B{D^2} = {8^2} + {10^2} - 2.8.10.\cos 88,{21^ \circ } \approx 159\\ \Rightarrow BD \approx 12,6\end{array}\)
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
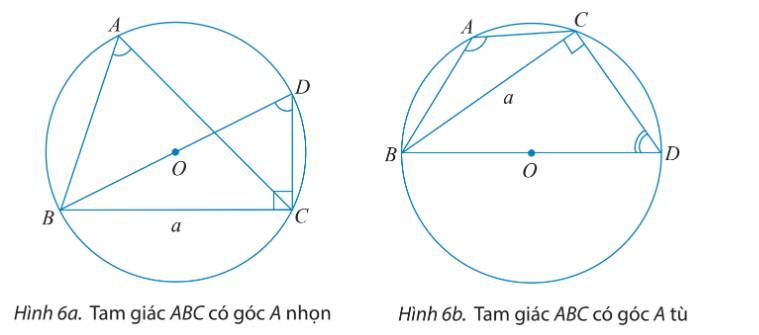
a) Tam giác BDC vuông tại C nên \(\sin \widehat {BDC} = \frac{{BC}}{{BD}} = \frac{a}{{2R}}.\)
b)
TH1: Tam giác ABC có góc A nhọn
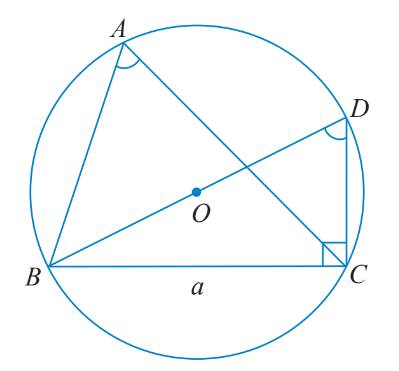
\(\widehat {BAC} = \widehat {BDC}\) do cùng chắn cung nhỏ BC.
\( \Rightarrow \sin \widehat {BAC} = \sin \widehat {BDC} = \frac{a}{{2R}}.\)
TH2: Tam giác ABC có góc A tù
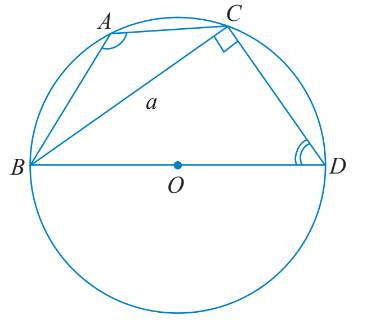
\(\widehat {BAC} + \widehat {BDC} = {180^o}\) do ABDC là tứ giác nội tiếp (O).
\( \Rightarrow \sin \widehat {BAC} = \sin ({180^o} - \widehat {BAC}) = \sin \widehat {BDC} = \frac{a}{{2R}}.\)
Vậy với góc A nhọn hay tù ta đều có \(2R = \frac{a}{{\sin A}}.\)
b) Nếu tam giác ABC vuông tại A thì BC là đường kính của (O).
Khi đó ta có: \(\sin A = \sin {90^o} = 1\) và \(a = BC = 2R\)
Do đó ta vẫn có công thức: \(2R = \frac{a}{{\sin A}}.\)
7 tháng 9 2023
Hình vẽ chỉ mang tính chất minh hoạ thôi nha bạn.
Trên tia đối của AB lấy điểm D sao cho \(BD\text{=}BC\)
Do đó :
Ta có : tam giác BDC cân tại B
\(AD\text{=}DB+AB\text{=}BC+AB\text{=}3AB\)
\(\Rightarrow\widehat{ABC}\text{=}\widehat{BDC}+\widehat{BCD}\text{=}2\widehat{BCD}\)
Mà : \(\widehat{B}\text{=}2\widehat{C}\) nên \(\widehat{B}\text{=}\widehat{DCA}\)
Xét \(\Delta BAC\) và \(\Delta CAD\) có :
\(\widehat{A}:gócchung\)
\(\widehat{B}\text{=}\widehat{ACD}\left(cmt\right)\)
\(\Rightarrow\Delta BAC\sim\Delta CAD\left(g-g\right)\)
\(\Rightarrow\dfrac{AB}{AC}\text{=}\dfrac{AC}{AD}\) \(\Rightarrow AC^2\text{=}AB.AD\)
Mà \(AD\text{=}3AB\) \(\Rightarrow AC^2\text{=}3AB^2\)
Ta có : \(BC^2\text{=}4AB^2\)
Xét tam giác ABC có : \(AB^2+AC^2\text{=}AB^2+3AB^2\text{=}4AB^2\text{=}BC^2\)
\(\Rightarrow\Delta ABC\) vuông tại A
Kết hợp với gt của đề bài : \(\Rightarrow\widehat{A}\text{=}90^o;\widehat{C}\text{=}30^o;\widehat{B}\text{=}60^o\).
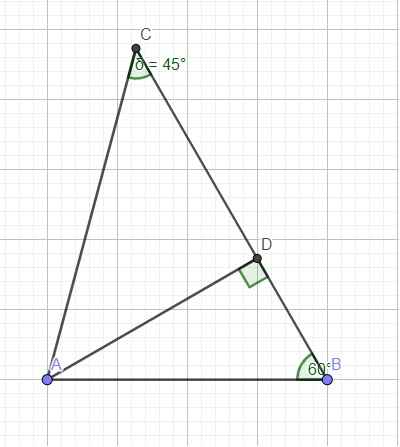
Trên BC lấy điểm D sao cho ^DAB = 300
^A = 1800 - (^B + ^C) = 750
Do đó D nằm trên cạnh BC và ^DAC = 750 - 300 = 450
Vẽ BE vuông góc AD tại E, CF vuông góc AD tại F
Ta có AB = 2BE và AC = \(\sqrt{2}\)CF
Do đó AB + \(\sqrt{2}\)AC = 2BC <=> BE + CF = BC <=> BE + CF = BD + CD
Mà BE \(\le\)BD và CF \(\le\)CD. Do vậy các dấu "=" xảy ra
<=> E, F, D trùng nhau <=> AD vuông góc BC
Do vậy ^B = 900 - 300 = 600 ; ^C = 900 - 450 = 450