Trên nửa đường tròn tâm O đường kính AB với AB = 2022, lấy điểm C (C khác A và B), từ C kẻ CH vuông góc với AB (H thuộc AB). Gọi D là điểm bất kỳ trên đoạn CH (D khác C và H), đường thẳng AD cắt nửa đường tròn tại điểm thứ hai là E. a) Chứng minh tứ giác BHDE là tứ giác nội tiếp; b) Chứng minh: AD.EC=CD.AC; c) Chứng minh: AD.AE+BH.BA=2022^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt chu vi COH là \(P=OC+OH+CH\)
Ta có:
\(P=OC+OH+CH\le OC+\sqrt{2\left(OH^2+CH^2\right)}=OC+\sqrt{2OC^2}=OC\left(1+\sqrt{2}\right)=R\left(1+\sqrt{2}\right)\)
Dấu "=" xảy ra khi \(OH=CH\Rightarrow\Delta OCH\) vuông cân tại H
\(\Rightarrow\widehat{COH}=45^0\) hay C là điểm nằm trên cung AB sao cho OC hợp với AB 1 góc 45 độ
//Phía trên sử dụng BĐT \(a+b\le\sqrt{2\left(a^2+b^2\right)}\) để đánh giá

a: góc AEB=1/2*180=90 dộ
góc DHB+góc DEB=180 độ
=>DHBE nội tiếp

a) Vì AB là đường kính \(\Rightarrow\angle ANB=90\)
\(\Rightarrow\angle FNB+\angle FCB=90+90=180\Rightarrow BCFN\) nội tiếp
b) Vì AB là đường kính \(\Rightarrow\angle ADB=90\)
Xét \(\Delta ACE\) và \(\Delta ADB:\) Ta có: \(\left\{{}\begin{matrix}\angle ADB=\angle ACE=90\\\angle BAEchung\end{matrix}\right.\)
\(\Rightarrow\Delta ACE\sim\Delta ADB\left(g-g\right)\Rightarrow\dfrac{AC}{AD}=\dfrac{AE}{AB}\Rightarrow AD.AE=AB.AC\)
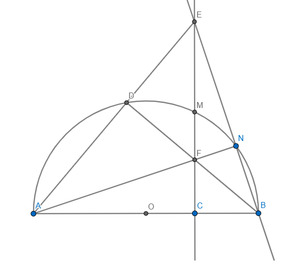

a: góc BNA=1/2*180=90 độ
góc FNB+góc FCB=180 độ
=>FCBN nội tiếp
b: góc ADB=1/2*180=90 độ
Xét ΔADB vuông tạiD và ΔACE vuông tại C có
góc A chung
=>ΔADB đồng dạng với ΔACE
=>AD/AC=AB/AE
=>AC*AB=AD*AE
c: Xét ΔEAB có
EC,AN là đường cao
EC cắt AN tại F
=>F là trực tâm
=>BF vuông góc AE
mà BD vuông góc AE
nên B,F,D thẳng hàng

A,D,N,B cùng thuộc (O)
nên ADNB nội tiếp
=>góc ADN+góc ABN=180 độ
=>góc EDN=góc EBA

A,D,N,B cùng thuộc (O)
nên ADNB nội tiếp
=>góc ADN+góc ABN=180 độ
=>góc EDN=góc EBA

a: góc EHB+góc EDB=180 độ
=>BDHE nội tiếp
b: Xét ΔACE và ΔADC có
góc ACE=góc ADC
góc CAE chung
=>ΔACE đồng dạng với ΔADC
=>AC^2=AE*AD
a.
\(DH\perp AB\left(gt\right)\Rightarrow\widehat{DHB}=90^0\Rightarrow D;H;B\) cùng thuộc đường tròn đường kính DB
\(\widehat{AEB}=90^0\) (góc nội tiếp chắn nửa đường tròn (O)) \(\Rightarrow\widehat{DEB}=90^0\)
\(\Rightarrow D;E;B\) cùng thuộc đường tròn đường kính DB
\(\Rightarrow\) Tứ giác BHDE nội tiếp đường tròn đường kính DB
b.
\(\widehat{ACB}=90^0\) (góc nội tiếp chắn nửa đường tròn (O))
\(\Rightarrow\widehat{ACH}=\widehat{ABC}\) (cùng phụ \(\widehat{BAC}\))
Mà \(\widehat{ABC}=\widehat{AEC}\) (cùng chắn cung AC của (O)
\(\Rightarrow\widehat{ACH}=\widehat{AEC}\)
Xét hai tam giác ADC và ACE có: \(\left\{{}\begin{matrix}\widehat{ACH}=\widehat{AEC}\left(cmt\right)\\\widehat{CAD}\text{ chung}\end{matrix}\right.\)
\(\Rightarrow\Delta ADC\sim\Delta ACE\left(g.g\right)\Rightarrow\dfrac{AD}{AC}=\dfrac{CD}{EC}\Rightarrow AD.EC=CD.AC\)
c.
Cũng theo cmt \(\Delta ADC\sim\Delta ACE\Rightarrow\dfrac{AC}{AE}=\dfrac{AD}{AC}\Rightarrow AD.AE=AC^2\)
Áp dụng hệ thức lượng trong tam giác vuông ABC với đường cao CH:
\(BC^2=BH.BA\)
\(\Rightarrow AD.AE+BH.BA=AC^2+BC^2=AB^2=2022^2\)