Viết chương trình nhập nhiệt độ h so với mặt đất của một vật rơi tại nơi có gia tốc g . Tính và hiển thi vận tốc của vật tại mặt đất
Tin hoc đấy nha
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TM
23 tháng 8 2023
\(s_2-s_1=40\Leftrightarrow s-s_1-s_1=40\Leftrightarrow s-2s_1=40\)
\(\Rightarrow\dfrac{1}{2}gt^2-2\cdot\dfrac{1}{2}gt_1^2=40\)
Mà: \(t_1=\dfrac{1}{2}t\Rightarrow\dfrac{1}{2}gt^2-2\cdot\dfrac{1}{2}g\left(\dfrac{1}{2}t\right)^2=40\)
\(\Leftrightarrow\dfrac{1}{4}gt^2=40\Leftrightarrow t=\sqrt{\dfrac{40}{\dfrac{1}{4}g}}=\sqrt{\dfrac{40}{\dfrac{1}{4}\cdot10}}=4\left(s\right)\)
\(\Rightarrow\left\{{}\begin{matrix}h=s=\dfrac{1}{2}gt^2=\dfrac{1}{2}\cdot10\cdot4^2=80\left(m\right)\\v=gt=10\cdot4=40\left(m/s\right)\end{matrix}\right.\)
Vậy: h = 80 (m), t = 4 (s) và v = 40 (m/s).
VT
13 tháng 9 2017
Quãng đường vật rơi nửa thời gian đầu:
Quãng đường vật rơi nửa thời gian cuối
Quãng đường vật rơi: h = h 1 + h 2
VT
18 tháng 10 2017
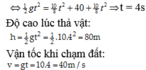
Đáp án D
Quãng đường vật rơi nửa thời gian đầu:
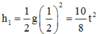
Quãng đường vật rơi nửa thời gian cuối
Quãng đường vật rơi:
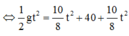
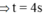
Độ cao lúc thả vật:
Vận tốc khi chạm đất:
v = gt = 10.4 = 40m/s
30 tháng 11 2021
Tại mặt đất: \(g_0=G\cdot\dfrac{M}{R^2}\)
Tại độ cao h: \(g=G\cdot\dfrac{M}{\left(R+h\right)^2}\)
Xét tỉ lệ:
\(\dfrac{g_0}{g}=\dfrac{\left(R+h\right)^2}{R^2}=\dfrac{9,81}{4,9}=2\)
\(\Rightarrow\dfrac{\left(R+h\right)^2}{R^2}=2\Rightarrow h=2650,97km\)
6 tháng 3 2022
Tóm tắt:
m = 400g = 0,4kg
h = 40m
g = 9,8m/s2
W = ?J
h' = ?m
v = ?m/s
Giải
a, W = Wt = m.g.h = 0,4 . 9,8 . 40 = 156,8 (J)
b, Wt = Wd
=> Wt = Wd = W/2 = 156,8/2 = 78,4 (J)
=> h' = Wt/(m.g) = 78,4/(0,4.9,8) = 20 (m)
c, Wt = 2.Wd
=> Wd = W/3 = 156,8/3 = 784/15 (J)
=> v2 = (Wd.2)/m = (784/15 . 2)/0,4 = 784/3
=> v = 16,165... (m/s)
Vật rơi:
Quảng đường đi được:
h = v0t + \(\frac{1}{2}\)gt2
v0 = 0
=> h = \(\frac{1}{2}\)gt2
=> t = \(\sqrt{\frac{2h}{g}}\)
Vận tốc khi chạm đất:
v = v0 + gt
v0 = 0
=> v = gt = g\(\sqrt{\frac{2h}{g}}\)= \(\sqrt{2gh}\)
Chương trình nhập vào g,h => tính được v = \(\sqrt{2gh}\)