giải phương trình x2 + x2/(x+1)2 =5/4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
2 tháng 6 2018
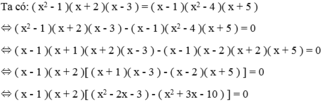
⇔ ( x - 1 )( x + 2 )( 7 - 5x ) = 0
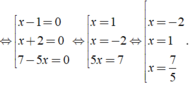
Vậy phương trình có tập nghiệm là S = { - 2; 1; 7/5 }.
NN
2
Y
11 tháng 4 2022
\(x^2-2x+1< 9\)
\(\Leftrightarrow\left(x-1\right)^2< 9\)
\(\Leftrightarrow x-1< 3\)
\(\Leftrightarrow x< 4\)
\(\left(x-1\right)\left(4-x^2\right)\ge0\)
\(\Leftrightarrow\left(x-1\right)\left(2-x\right)\left(2+x\right)\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\2-x=0\\2+x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\\x=-2\end{matrix}\right.\)
\(\dfrac{x+2}{x-5}< 0\)
\(\Leftrightarrow x+2< 0\)
\(\Leftrightarrow x< -2\)
11 tháng 4 2022
a)\(x^2-2x+1< 9\)
\(\Leftrightarrow\left(x-1\right)^2< 9\)
\(\Leftrightarrow\left(x-1\right)^2-9< 0\)
\(\Leftrightarrow\left(x-1-3\right)\left(x-1+3\right)< 0\)
\(\Leftrightarrow\left(x-4\right)\left(x+2\right)< 0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-4< 0\\x+2>0\end{matrix}\right.hay\left[{}\begin{matrix}x-4>0\\x+2< 0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x< 4\\x>-2\end{matrix}\right.hay\left[{}\begin{matrix}x>4\\x< -2\end{matrix}\right.\)(vô lý)
-Vậy nghiệm của BĐT là \(-2< x< 4\).
b) \(\left(x-1\right)\left(4-x^2\right)\ge0\)
\(\Leftrightarrow\left(x-1\right)\left(2-x\right)\left(x+2\right)\ge0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)\left(x+2\right)\le0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1< 0\\x-2>0\\x+2>0\end{matrix}\right.\) hay \(\left[{}\begin{matrix}x-1>0\\x-2< 0\\x+2>0\end{matrix}\right.\) hay \(\left[{}\begin{matrix}x-1>0\\x-2 >0\\x+2< 0\end{matrix}\right.\) hay \(\left[{}\begin{matrix}x-1< 0\\x-2< 0\\x+2< 0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x< 1\\x>2\\x>-2\end{matrix}\right.\) (vô lí) hay \(\left[{}\begin{matrix}x>1\\x< 2\\x>-2\end{matrix}\right.\) (có thể xảy ra) hay
\(\left[{}\begin{matrix}x>1\\x>2\\x< -2\end{matrix}\right.\) (vô lí) hay \(\left[{}\begin{matrix}x< 1\\x< 2\\x< -2\end{matrix}\right.\) (có thể xảy ra)
-Vậy nghiệm của BĐT là \(x< -2\) hay \(1< x< 2\).
c) ĐKXĐ: \(x\ne5\)
\(\dfrac{x+2}{x-5}< 0\Leftrightarrow\left[{}\begin{matrix}x+2< 0\\x-5>0\end{matrix}\right.hay\left[{}\begin{matrix}x+2>0\\x-5< 0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x< -2\\x>5\end{matrix}\right.\)(vô lí) hay
\(\left[{}\begin{matrix}x>-2\\x< 5\end{matrix}\right.\) (có thể xảy ra)
-Vậy nghiệm của BĐT là \(-2< x< 5\)
10 tháng 5 2021
a) Với m = 5 phương trình đã cho trở thành
x2 - 8x + 7 = 0
Dễ thấy phương trình trên có a + b + c = 0 nên có hai nghiệm phân biệt x1 = 1 ; x2 = c/a = 7
Vậy với m = 5 thì phương trình đã cho có tập nghiệm S = { 1 ; 7 }
b) Ta có : Δ = b2 - 4ac = [ -2( m - 1 ) ]2 - 4( m + 2 )
= 4( m2 - 2m + 1 ) - 4m + 8
= 4m2 - 12m + 12 = 4( m - 3/2 )2 + 3 ≥ 3 > 0 ∀ m
=> Phương trình đã cho luôn có hai nghiệm phân biệt với mọi số thực m
Theo hệ thức Viète ta có : \(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}=2m-2\\x_1x_2=\frac{c}{a}=m+2\end{cases}}\)
Ta có : \(\frac{x_1}{x_2}+\frac{x_2}{x_1}=4\Leftrightarrow\frac{x_1^2}{x_1x_2}+\frac{x_2^2}{x_1x_2}=4\)
\(\Rightarrow x_1^2+x_2^2=4x_1x_2\Leftrightarrow\left(x_1+x_2\right)^2-6x_1x_2=0\)
\(\Rightarrow\left(2m-2\right)^2-6\left(m+2\right)=0\)
\(\Leftrightarrow4m^2-8m+4-6m-12=0\Leftrightarrow2m^2-7m-4=0\)
Đến đây dễ rồi bạn tự làm tiếp heng :)
18 tháng 7 2021
\(a,=>x^3-2x^2+4x+2x^2-4x+8-x^3+2x-15=0\)
\(< =>2x-7=0< =>x=\dfrac{7}{2}\)
b,\(=>x\left(x^2-25\right)-\left(x+2\right)\left(x^2-2x+4\right)-3=0\)
\(< =>x^3-25x-x^3+2x^2-4x-2x^2+4x-8-3=0\)
\(< =>-25x-11=0\)
\(< =>x=-0,44\)
TG
16 tháng 1 2021
a) \(x^2+2x=\left(x-2\right).3x\)
\(\Leftrightarrow x^2+2x=3x^2-6x\)
\(\Leftrightarrow x^2+2x-3x^2+6x=0\)
\(\Leftrightarrow-2x^2+8x=0\)
\(\Leftrightarrow-2x\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}-2x=0\\x-4=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
Vậy S = {0;4}
b) \(x^3+x^2-x-1=0\)
\(\Leftrightarrow x^2\left(x+1\right)-\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x^2-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\x^2-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^2=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\mp1\end{matrix}\right.\)
Vậy: S = {-1; 1}
c) \(\left(x+1\right)\left(x+2\right)\left(x+4\right)\left(x+5\right)=40\)
\(\Leftrightarrow\left[\left(x+1\right)\left(x+5\right)\right]\left[\left(x+2\right)\left(x+4\right)\right]=40\)
\(\Leftrightarrow\left(x^2+5x+x+5\right)\left(x^2+4x+2x+8\right)=40\)
\(\Leftrightarrow\left(x^2+6x+5\right)\left(x^2+6x+8\right)=40\)
Đặt x2 + 6x + 5 = t
\(\Leftrightarrow t.\left(t+3\right)=40\)
\(\Leftrightarrow t^2+3t=40\)
\(\Leftrightarrow t^2+2.t.\dfrac{3}{2}+\dfrac{9}{4}=\dfrac{169}{4}\)
\(\Leftrightarrow\left(t+\dfrac{3}{2}\right)^2=\dfrac{169}{4}\)
\(\Leftrightarrow\left[{}\begin{matrix}t+\dfrac{3}{2}=\dfrac{13}{2}\\t+\dfrac{3}{2}=-\dfrac{13}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}t=\dfrac{13}{2}-\dfrac{3}{2}=\dfrac{10}{2}=5\\t=-\dfrac{13}{2}-\dfrac{3}{2}=-\dfrac{16}{2}=-8\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+6x+5=5\\x^2+6x+5=-8\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2+6x=0\\x^2+6x+13=0\end{matrix}\right.\)
Mà: \(x^2+6x+13=x^2+2.x.3+9+4=\left(x+3\right)^2+4\ne0\)
=> x2 + 6x = 0
<=> x. (x + 6) = 0
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+6=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-6\end{matrix}\right.\)
Vậy S = {0; -6}
16 tháng 1 2021
a) Ta có: \(x^2+2x=\left(x-2\right)\cdot3x\)
\(\Leftrightarrow x\left(x+2\right)-3x\left(x-2\right)=0\)
\(\Leftrightarrow x\left[\left(x+2\right)-3\left(x-2\right)\right]=0\)
\(\Leftrightarrow x\left(x+2-3x+6\right)=0\)
\(\Leftrightarrow x\left(-2x+8\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\-2x+8=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\-2x=-8\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)
Vậy: S={0;4}
b) Ta có: \(x^3+x^2-x-1=0\)
\(\Leftrightarrow x^2\left(x+1\right)-\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\cdot\left(x^2-1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\cdot\left(x-1\right)\cdot\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)^2\cdot\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(x+1\right)^2=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x+1=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
Vậy: S={-1;1}
c) Ta có: \(\left(x+1\right)\left(x+2\right)\left(x+4\right)\left(x+5\right)=40\)
\(\Leftrightarrow\left(x+1\right)\left(x+5\right)\left(x+2\right)\left(x+4\right)-40=0\)
\(\Leftrightarrow\left(x^2+6x+5\right)\left(x^2+6x+8\right)-40=0\)
\(\Leftrightarrow\left(x^2+6x\right)^2+13\left(x^2+6x\right)+40-40=0\)
\(\Leftrightarrow\left(x^2+6x\right)^2+13\left(x^2+6x\right)=0\)
\(\Leftrightarrow\left(x^2+6x\right)\left(x^2+6x+13\right)=0\)
\(\Leftrightarrow x\left(x+6\right)\left(x^2+6x+13\right)=0\)
mà \(x^2+6x+13>0\forall x\)
nên \(x\left(x+6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-6\end{matrix}\right.\)
Vậy: S={0;-6}
HP
11 tháng 1 2022
\(a.\left(3x+2\right)\left(x^2-1\right)=\left(9x^2-4\right)\left(x+1\right)\)
\(\Leftrightarrow\left(3x+2\right)\left(x+1\right)\left(x-1\right)=\left(3x-2\right)\left(3x+2\right)\left(x+1\right)\)
\(\Leftrightarrow x-1=3x-2\)
\(\Leftrightarrow2x=1\)
\(\Leftrightarrow x=\dfrac{1}{2}\)
11 tháng 1 2022
c: =>x-3=0
hay x=3
d: \(\Leftrightarrow\left(3x-1\right)\cdot\left(x^2+2-7x+10\right)=0\)
\(\Leftrightarrow\left(3x-1\right)\left(x-3\right)\left(x-4\right)=0\)
hay \(x\in\left\{\dfrac{1}{3};3;4\right\}\)
11 tháng 1 2022
\(\left(3x+2\right)\left(x^2-1\right)=\left(9x^2-4\right)\left(x+1\right).\)
\(\Leftrightarrow\left(3x+2\right)\left(x-1\right)\left(x+1\right)-\left(3x-2\right)\left(3x+2\right)\left(x+1\right)=0.\)
\(\Leftrightarrow\left(3x+2\right)\left(x+1\right)\left(x-1-3x+2\right)=0.\)
\(\Leftrightarrow\left(3x+2\right)\left(x+1\right)\left(-2x+1\right)=0.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+2=0.\\x+1=0.\\-2x+1=0.\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{2}{3}.\\x=-1.\\x=\dfrac{1}{2}.\end{matrix}\right.\)
11 tháng 1 2022
c: =>(x-3)(x2+3x+5)=0
=>x-3=0
hay x=3
d: =>(3x-1)(x2+2-7x+10)=0
=>(3x-1)(x-3)(x-4)=0
hay \(x\in\left\{\dfrac{1}{3};3;4\right\}\)
AH
Akai Haruma
Giáo viên
24 tháng 8 2023
1. Đặt $x^2+x=a$ thì pt trở thành:
$a^2+4a=12$
$\Leftrightarrow a^2+4a-12=0$
$\Leftrightarrow (a-2)(a+6)=0$
$\Leftrightarrow a-2=0$ hoặc $x+6=0$
$\Leftrightarrow x^2+x-2=0$ hoặc $x^2+x+6=0$
Dễ thấy $x^2+x+6=0$ vô nghiệm.
$\Rightarrow x^2+x-2=0$
$\Leftrightarrow (x-1)(x+2)=0$
$\Leftrightarrow x=1$ hoặc $x=-2$
AH
Akai Haruma
Giáo viên
24 tháng 8 2023
2.
$x(x-1)(x+1)(x+2)=24$
$\Leftrightarrow [x(x+1)][(x-1)(x+2)]=24$
$\Leftrightarrow (x^2+x)(x^2+x-2)=24$
$\Leftrightarrow a(a-2)=24$ (đặt $x^2+x=a$)
$\Leftrightarrow a^2-2a-24=0$
$\Leftrightarrow (a+4)(a-6)=0$
$\Leftrightarrow a+4=0$ hoặc $a-6=0$
$\Leftrightarrow x^2+x+4=0$ hoặc $x^2+x-6=0$
Nếu $x^2+x+4=0$
$\Leftrightarrow (x+\frac{1}{2})^2=\frac{1}{4}-4<0$ (vô lý - loại)
Nếu $x^2+x-6=0$
$\Leftrightarrow (x-2)(x+3)=0$
$\Leftrightarrow x-2=0$ hoặc $x+3=0$
$\Leftrightarrow x=2$ hoặc $x=-3$
A4
1
16 tháng 1 2021
\(a,\left(2x-3\right)^2=\left(x+1\right)^2\\ \Leftrightarrow\left(2x-3\right)^2-\left(x+1\right)^2=0\\ \Leftrightarrow\left(2x-3+x+1\right)\left(2x-3-x-1\right)=0\\ \Leftrightarrow\left(3x-2\right)\left(x-4\right)\\ \Leftrightarrow\left[{}\begin{matrix}3x-2=0\\x-4=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}3x=2\\x=4\end{matrix}\right. \\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=4\end{matrix}\right.\)
Vậy \(x\in\left\{\dfrac{2}{3};4\right\}\)
16 tháng 1 2021
\(b,x^2-6x+9=9\left(x-1\right)^2\\ \Leftrightarrow\left(x-3\right)^2=9\left(x-1\right)^2\\ \Leftrightarrow\left(x-3\right)^2-9\left(x-1\right)^2=0\\ \Leftrightarrow\left(x-3\right)^2-3^2\left(x-1\right)^2=0\\ \Leftrightarrow\left(x-3\right)^2-\left[3\left(x-1\right)\right]^2=0\\ \Leftrightarrow\left(x-3\right)^2-\left(3x-3\right)^2=0\\ \Leftrightarrow\left(x-3+3x-3\right)\left(x-3-3x+3\right)=0\\ \Leftrightarrow-2x\left(4x-6\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}-2x=0\\4x-6=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\4x=6\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{3}{2}\end{matrix}\right.\)
Vậy \(x\in\left\{0;\dfrac{3}{2}\right\}\)