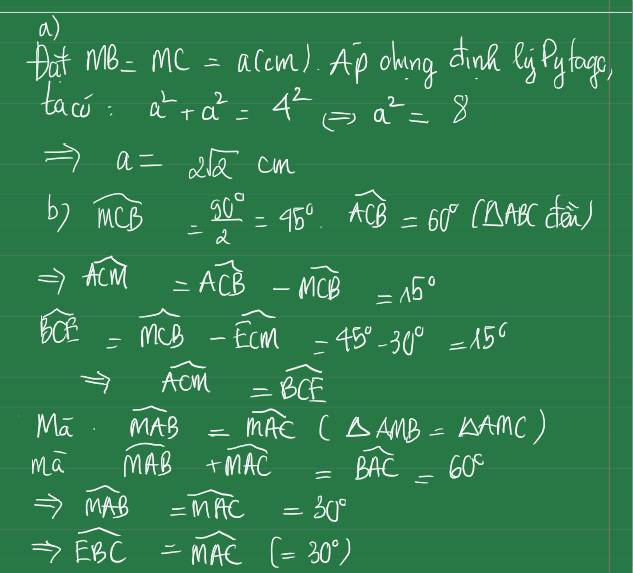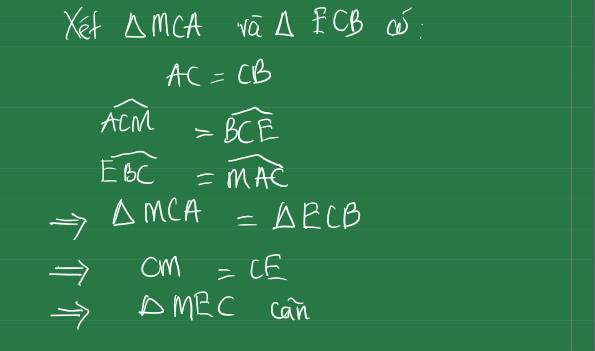cho tam giác ABC có A=90' có AB=3AC và tồn tại điểm M sao cho Ma:MB:MC=1:4:căn 2. tính góc BMC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 4 2017
bạn chơi bang bang ak mà chụp hình ảnh kiếm thần nên có nick bang bang cho mình một nick nhé mình giải bài này cho
10 tháng 7 2019
Câu hỏi của channel Anhthư - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo nhé!
19 tháng 8 2017
Vẽ tam giác MBK vuông cân tại B (K và A nằm cùng phía đối với BM) . Đặt MA = a , MB =2a, MC=3a.
Tam giác ABK= tam giác CBK(c.g.c)
Suy ra AK=CM=3a
Xét tam giác MBK vuông cân tại B:
MK2=MB2+BK2 =(2a)2 + (2a)2=8a2
Xét tam giác AMK ta có:
MA2 +MK2 = a2 + 8a2 =9a2 =AK2
nên góc AMK = 900 (định lí Pi ta go đảo)
Vậy góc AMB = 1350
NT
0
10 tháng 7 2019
Em tham khảo link này nhé!
Câu hỏi của channel Anhthư - Toán lớp 7 - Học toán với OnlineMath
1 tháng 12 2018
1, Ta có \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)(tổng 3 góc tam giác)
\(\Leftrightarrow\widehat{C}+90^o+\widehat{C}=180^o\)
\(\Leftrightarrow2\widehat{C}=90^o\)
\(\Leftrightarrow\widehat{C}=45^o\)
\(\Rightarrow\widehat{A}=\widehat{C}+10=55^o\)
\(\Rightarrow\widehat{B}=180^o-\widehat{A}-\widehat{C}=180^o-55^o-45^o=80^o\)
1 tháng 12 2018
2,
A B C M 1 1
Vì tam giác ABC vuông tại A
=> ^B + ^C = 90o
Vì BM là phân giác ^ABC
=>^B1 = \(\frac{\widehat{ABC}}{2}\)
Tương tự ^C1 = \(\frac{\widehat{ACB}}{2}\)
\(\Rightarrow\widehat{B_1}+\widehat{C_1}=\frac{\widehat{ABC}+\widehat{ACB}}{2}=\frac{90^o}{2}=45^o\)
Theo tổng 3 góc trong tam giác \(\widehat{BMC}=180^o-\widehat{B_1}-\widehat{C_1}=180^o-45^o=135^o\)