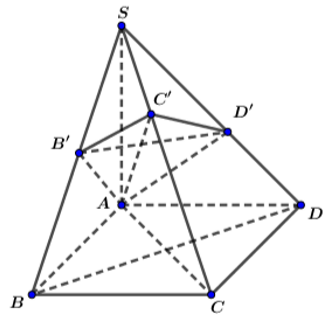
Giúp mk cái bài hình kia trong trường hợp vuông góc SC với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HH
26 tháng 5 2018
a/ \(\Delta ADE\)vuông và \(\Delta ADF\)vuông có:
\(\widehat{EAD}=\widehat{DAF}\)(AD là đường phân giác của \(\Delta ABC\))
Cạnh huyền AD chung
=> \(\Delta ADE\)vuông = \(\Delta ADF\)vuông (cạnh huyền - góc nhọn)
=> DE = DF (hai cạnh tương ứng) (đpcm)
b/ \(\Delta ABD\)và \(\Delta ACD\)có:
AB = AC (\(\Delta ABC\)cân tại A)
\(\widehat{EAD}=\widehat{DAF}\)(AD là đường phân giác của \(\Delta ABC\))
Cạnh AD chung
=> \(\Delta ABD\)= \(\Delta ACD\)(c. g. c)
Ta có AB = AC (\(\Delta ABC\)cân tại A)
=> A thuộc đường trung trực của BC
=> AD \(\perp\)BC (đpcm)
c/ Ta có AD là đường phân giác của \(\Delta ABC\)
=> \(\widehat{DAB}=\frac{\widehat{BAC}}{2}=\frac{80^o}{2}=40^o\)(tính chất tia phân giác)
và \(\widehat{EDA}=90^o-\widehat{DAB}\)(\(\Delta ADB\)vuông tại D)
=> \(\widehat{EDA}=90^o-40^o=50^o\)
Ta lại có: \(\widehat{DAB}< \widehat{EDA}\)(vì 40o < 50o)
=> DE < AE (quan hệ giữa góc và cạnh đối diện trong tam giác)
và \(\hept{\begin{cases}DA< AE\\DA< DE\end{cases}}\)(quan hệ giữa đường vuông góc và đường xiên)
=> DA < DE < AE (đpcm)
26 tháng 5 2018
a)Xét tam giác EAD và FAD có
AÊD= góc AFD=90*
AD là cạnh chung
góc EAD=góc FAD(tam giác ABC cân)
=>tam giác ...=...(cạnh huyền-góc nhọn)
=>DE=DF
b)Xét tam giác ABD và ACD có
BA=CA(gt)
BÂD=CÂD(gt)
AD là cạnh chung
=>tam giác ...=...(c-g-c)
=>góc BDA=CDA
mà BDA+CDA=180*
=>BDA=CDA=180*/2=90*
=>AD vuông góc với BC
c) Xét tam giác AED có: AÊD+EÂD+ góc EDA=180*
=>90*+(80*/2)+góc EAD=180*
=>90*+40*+góc EAD=180*
=>góc EAD=180*-(90*+40*)
=>góc EAD=50*
ta có:EÂD<góc ADE<AÊD(40*<50*<90*)
=>ED<AE<AD
Vậy, ED<AE<AD.
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
\(ABCD\) là hình chữ nhật (gt)
Suy ra \(AB = CD\); \(AD = BC\); \(AB\) // \(CD\); \(AD\) // \(BC\) (3)
\(\widehat A = \widehat B = \widehat C = \widehat D = 90^\circ \) (1)
TH1:
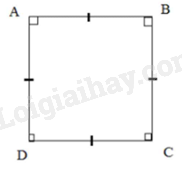
Nếu \(AB = BC\) (gt) thì \(AB = BC = CD = DA\) (2)
Từ (1), (2) suy ra \(ABCD\) là hình vuông
TH2:
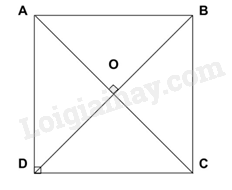
Nếu \(AC\) vuông góc với \(BD\)
Mà \(ABCD\) cũng là hình bình hành
Suy ra \(ABCD\) là hình thoi
Suy ra \(AB = BC = CD = DA\) (4)
Từ (1) và (4) suy ra \(ABCD\) là hình vuông
TH3:
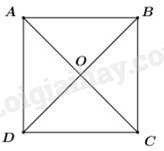
\(AC\) là phân giác của góc \(BAD\)
Mà \(ABCD\) là hình bình hành
Suy ra \(ABCD\) là hình thoi
Suy ra \(AB = BC = CD = DA\) (5)
Từ (1) và (5) suy ra \(ABCD\) là hình vuông
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 2 2023
Đề bài thiếu dữ liệu định vị điểm S (ví dụ SC bằng bao nhiêu đó) nên ko thể tính góc giữa SB và (ABCD)