Tam giác abc đường cao ah biết ab=9 bc=15 tính chu vi và diện tích tam giác abh
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
11 tháng 9 2021
Lời giải:
Vì $AB: AC=3:7$ nên đặt $AB=3a; AC=7a$. Áp dụng hệ thức lượng trong tam giác vuông:
$\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}$
$\frac{1}{42^2}=\frac{1}{(3a)^2}+\frac{1}{(7a)^2}$
$\frac{1}{42^2}=\frac{58}{441a^2}$
$\Rightarrow a=2\sqrt{58}$ (cm)
$AB=3a=6\sqrt{58}$ (cm)
$BH=\sqrt{AB^2-AH^2}=\sqrt{(6\sqrt{58})^2-42^2}=18$ (cm)
Chu vi $ABH$: $AB+BH+AH=6\sqrt{58}+18+42=60+6\sqrt{58}$ (cm)
$AC=7a=14\sqrt{58}$ (cm)
$HC=\sqrt{AC^2-AH^2}=\sqrt{(14\sqrt{58})^2-42^2}=98$ (cm)
$S_{AHC}=\frac{AH.HC}{2}=\frac{42.98}{2}=2058$ (cm vuông)
30 tháng 12 2022
\(BC=\dfrac{15^2}{9}=25\left(cm\right)\)
BH=25-9=16cm
\(AH=\sqrt{9\cdot16}=12\left(cm\right)\)
AB=căn(16^2+12^2)=20cm
C=16+12+20=28+20=48cm
Xét ΔABC vuông tại A có sin B=AC/BC=3/5
nên góc B=37 độ
CM
18 tháng 6 2017
Áp dụng định lý Pytago trong ∆ ABC vuông tại A ta có:
Áp dụng hệ thức lượng trong ∆ ABC vuông tại A có đường cao AH ta có:
Đáp án cần chọn là: B
5 tháng 7 2023
a: Xét ΔABH vuông tại H và ΔCBA vuông tại A có
góc B chung
=>ΔABH đồng dạng với ΔCBA
b:AB=căn 3,6*10=6(cm)
c: Xét ΔHAB vuông tại H và ΔHCA vuông tại H có
góc HAB=góc HCA
=>ΔHAB đồng dạng với ΔHCA
=>S HAB/S HCA=(AB/CA)^2
8 tháng 8 2023
a: AB=căn 5^2-4^2=3cm
Xét ΔABC vuông tại A có AH là đường cao
nên AB^2=BH*BC; AC^2=CH*BC; AH*BC=AB*AC
=>AH=3*4/5=2,4cm; BH=3^2/5=1,8cm
CH=5-1,8=3,2cm
b: C=3+4+5=12cm
S=1/2*3*4=6cm2
AM=BC/2=2,5cm
c: MA=MC=2,5cm
AC=4cm
ΔMAC cân tại M có MI là đường cao
nên I là trung điểm của AC
=>IA=IC=AC/2=2cm
MI=căn MA^2-IA^2=1,5cm
TT
25 tháng 5 2021
\(\Delta ABH\sim\Delta CAH\)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{C_{ABC}}{C_{CAH}}=\dfrac{30}{40}=\dfrac{3}{4}\)
=> \(\dfrac{AB^2}{9}=\dfrac{AC^2}{16}=\dfrac{BC^2}{25}\)
\(\Rightarrow\dfrac{AB}{3}=\dfrac{AC}{4}=\dfrac{BC}{5}\\\)
=> \(\dfrac{AB}{BC}=\dfrac{3}{5}\)
\(\Delta ABH\sim\Delta CBA\)
\(\Rightarrow\dfrac{C_{ABH}}{C_{ABC}}=\dfrac{AB}{BC}\)
=> Chu vi tam giác ABC là 30 . 5 : 3 = 50
25 tháng 5 2021
Gọi a, b, c lần lượt là chu vi của các tam giác ABC, ABH, ACH.
Ta có: b = 30cm, c = 40cm
Xét hai tam giác vuông AHB và CHA, ta có:
22 tháng 8 2020
Bài 1 Giải
Chu vi HCN là:
(12+8).2= 40(cm)
Diện tích HCN là:
12.8= 96(cm)
Bài 2 Chu vi hình vuông là:
20.4=80(cm)
Mà chu vi hình vuông bằng chu vi HCN nên:
Chiều rộng HCN là:
(80:2) -25=15(cm)
Diện tích HCN là:
15.25=375(cm)
Bài 3 Độ dài cạnh BC là:
120:10.2=24(cm)
Bài 4 Diện tích tam giác ABC là:
( 5.8):2 = 20(cm)
Chúc bn hok tốt~~
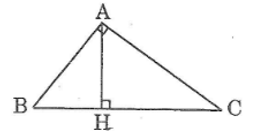
\(AC=\sqrt{15^2-9^2}=12\left(cm\right)\)
AH=9*12/15=7,2cm
BH=9^2/15=5,4cm
\(C_{ABH}=7.2+5.4+9=21.6\left(cm\right)\)
\(S_{ABH}=\dfrac{1}{2}\cdot5.4\cdot7.2=3.6\cdot5.4=19.44\left(cm^2\right)\)