Tìm m để phương trình x2 -mx+m-1=0 có hai nghiệm phân biệt x1 ,x2 thỏa mãn x12 +3x2=19...
Đọc tiếp
Tìm m để phương trình x2 -mx+m-1=0 có hai nghiệm phân biệt x1 ,x2 thỏa mãn x12 +3x2=19 .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 8 2021
\(a,m=3=>x^2+3x-2=0\)
\(\Delta=3^2-4\left(-2\right)=17>0\)
pt có 2 nghiệm pb \(\left[{}\begin{matrix}x1=\dfrac{-3+\sqrt{17}}{2}\\x2=\dfrac{-3-\sqrt{17}}{2}\end{matrix}\right.\)
b,\(\Delta=m^2-4\left(-2\right)=m^2+8>0\)
=> pt đã cho luôn có 2 nghiệm phân biệt x1,x2 với mọi m
theo vi ét \(\left\{{}\begin{matrix}x1+x2=-m\\x1x2=-2\end{matrix}\right.\)
có \(x1^2x2+x2^2x1=2014< =>x1x2\left(x1+x2\right)=2014\)
\(< =>-2\left(-m\right)=2014< =>m=1007\)
4 tháng 8 2021
a) Thay m=3 vào phương trình, ta được:
\(x^2+3x-2=0\)
\(\Delta=3^2-4\cdot1\cdot\left(-2\right)=9+8=17\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-3-\sqrt{17}}{2}\\x_2=\dfrac{-3+\sqrt{17}}{2}\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 1 2022
\(\Delta'=1-\left(m-3\right)=4-m>0\Rightarrow m< 4\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\\x_1x_2=m-3\end{matrix}\right.\)
Do \(x_1+x_2=2\Rightarrow x_2=2-x_1\)
Ta có:
\(x_1^2+x_1x_2=2x_2-12\)
\(\Leftrightarrow x_1\left(x_1+x_2\right)=2\left(2-x_1\right)-12\)
\(\Leftrightarrow2x_1=4-2x_1-12\)
\(\Leftrightarrow4x_1=-8\Rightarrow x_1=-2\Rightarrow x_2=4\)
Thế vào \(x_1x_2=m-3\Rightarrow m-3=-8\)
\(\Rightarrow m=-5\)
NT
1
AH
Akai Haruma
Giáo viên
26 tháng 2 2022
Tham khảo lời giải tại đây:
https://hoc24.vn/cau-hoi/tim-m-de-phuong-trinh-x2-7x-m-2-0-co-nghiem-x1-x2-thoa-man-x12-3x2-3.4915847121620
LD
1
AH
Akai Haruma
Giáo viên
26 tháng 2 2022
Lời giải:
Để pt có nghiệm thì: $\Delta=49-4(m-2)\geq 0$
$\Leftrightarrow m\leq 14,25$
Khi đó, áp dụng định lý Viet: $x_1+x_2=7; x_1x_2=m-2$
Để $x_1^2+3x_2=-3$
$\Leftrightarrow (7-x_2)^2+3x_2+3=0$
$\Leftrightarrow x_2^2-11x_2+52=0$
$\Leftrightarrow (x_2-5,5)^2=-21,75<0$ (vô lý)
Vậy không tồn tại $m$ thỏa điều kiện đề bài.
MH
31 tháng 1 2023
\(x^2-2\left(m+1\right)x+4m=0\)
\(\text{∆}=4\left(m+1\right)^2-16m=4\left(m-1\right)^2\)
để phương trình có 2 nghiệm phân biệt:
\(\Leftrightarrow\left(m-1\right)^2>0\Leftrightarrow m\ne1\)
\(\Rightarrow\left\{{}\begin{matrix}x_1=\dfrac{2\left(m+1\right)+2\left(m-1\right)}{2}=2m\\x_2=\dfrac{2\left(m+1\right)-2\left(m-1\right)}{2}=2\end{matrix}\right.\)
Ta có:
\(x_1=-3x_2\)
\(\Rightarrow2m=-6\Rightarrow m=-3\left(TM\right)\)
Vậy ...
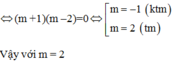
x1^2+x2^2=(x1+x2)^2-2x1x2
=m^2-2(m-1)=m^2-2m+2
=>x1^2=m^2-2m+2-x2^2
x1^2+3x2=19
=>m^2-2m+2-x2^2+3x2=19
=>-x2^2+3x2+m^2-2m-17=0
=>x2^2-3x2-m^2+2m+17=0(1)
Để (1) có nghiệm thì Δ1>0
=>(-3)^2-4*1*(-m^2+2m+17)>0
=>9-4(-m^2+2m+17)>0
=>9+4m^2-8m-68>0
=>4m^2-8m-59>0
=>\(\left[{}\begin{matrix}m< \dfrac{2-3\sqrt{7}}{2}\\m>\dfrac{2+3\sqrt{7}}{2}\end{matrix}\right.\)