Hai dây dẫn thẳng dài mang 2 dòng điện ngược chiều, đặt tại 2 điểm A, B có I1=6A, I2=9A đặt cách nhau 18cm trong không khí. a) Xác định cảm ứng từ do 2 dòng điện gây ra tại trung điểm C của AB b) Tính lực từ tác dụng lên mỗi mét chiều dài của 2 dây c) Tìm những vĩ trí mà tại đó cảm ứng từ tổng hợp = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
14 tháng 4 2018
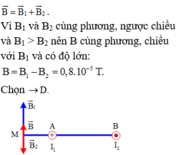
Giả sử hai dây dẫn được đặt vuông góc với mặt phẳng hình vẽ, dòng I 1 đi vào tại A, dòng I 2 đi ra tại B thì các dòng điện I 1 và I 2 gây ra tại M các véc tơ cảm ứng từ B 1 → và B 2 → có phương chiều như hình vẽ.
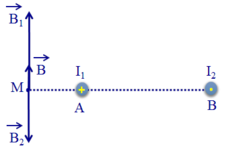
Có độ lớn: B 1 = 2 . 10 - 7 . I 1 A M = 2 , 4 . 10 - 5 T ; B 2 = 2 . 10 - 7 . I 2 B M = 1 , 6 . 10 - 5 T .
Cảm ứng từ tổng hợp tại M là: B → = B 1 → + B 2 → . Vì B 1 → và B 2 → cùng phương, ngược chiều và B 1 > B 2 nên B → cùng phương, chiều với B 1 → và có độ lớn:
B = B 1 - B 2 = 0 , 8 . 10 - 5 T .
VT
2 tháng 3 2019
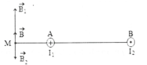
Giả sử hai dây dẫn được đặt vuông góc với mặt phẳng hình vẽ, dòng I1 đi vào tại A, dòng I2 đi ra tại B thì các dòng điện I1 và I2 gây ra tại M các vectơ cảm ứng từ B 1 → v à B 2 → có phương chiều như hình vẽ, có độ lớn:
VT
13 tháng 8 2019
Giả sử hai dây dẫn được đặt vuông góc với mặt phẳng hình vẽ, dòng I 1 đi vào tại A, dòng I 2 đi vào tại B. Tam giác AMB vuông tại M. Các dòng điện I 1 và I 2 gây ra tại M các véc tơ cảm ứng từ B 1 → và B 2 → có phương chiều như hình vẽ.
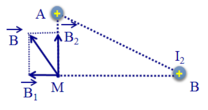
Có độ lớn: B 1 = 2 . 10 - 7 . I 1 A M = 3 . 10 - 5 T ; B 2 = 2 . 10 - 7 . I 2 B M = 4 . 10 - 5 T .
Cảm ứng từ tổng hợp tại M là: B → = B 1 → + B 2 → có phương chiều như hình vẽ và có độ lớn: B = B 1 2 + B 2 2 = 5 . 10 - 5 T .
VT
17 tháng 3 2018
Lời giải
+ Giả sử hai dầy dẫn đó được đặt vuông góc với mặt phẳng hình vẽ, dòng I 1 đi vào tại A, dòng I 2 đi ra tại B thì các dòng điện I 1 và gây ra I 2 tại M các véc tơ cảm ứng từ B → 1 và B → 2 có phương chiều như hình vẽ, có độ lớn:
a/ \(B_A=2.10^{-7}.\dfrac{I_1}{\dfrac{AB}{2}}=...\left(T\right);B_B=2.10^{-7}.\dfrac{I_2}{\dfrac{AB}{2}}=...\left(T\right)\)
\(B_A\uparrow\uparrow B_B\Rightarrow\sum B=B_A+B_B=...\left(T\right)\)
b/ \(F=\dfrac{2.10^{-7}.I_AI_B}{AB}.l=1.2.10^{-7}.\dfrac{6.9}{0,18}=...\left(N\right)\)
c/ \(\sum B=0\Leftrightarrow\left\{{}\begin{matrix}\overrightarrow{B_A}\uparrow\downarrow\overrightarrow{B_B}\\B_A=B_B\end{matrix}\right.\)
\(B_A=2.10^{-7}.\dfrac{I_A}{AM};B_B=2.10^{-7}.\dfrac{I_B}{AB+AM}\)
\(B_A=B_B\Leftrightarrow\dfrac{I_A}{AM}=\dfrac{I_B}{AB+AM}\Leftrightarrow AM=....\)