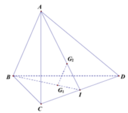
Cho tứ diện ABCD có G1.G2 lần lượt là trọng tâm của hai tam giác ABC và BCD. Hỏi trong ba khẳng định sau có bao nhiêu khẳng định đúng? (I) Ba vectơ AB, AC, AD. không đồng phẳng, (II) Ba vectơ AC, CD. G,G, đồng phẳng, (III) DA+DB+DC=30G, A. 1. B. 0. C. 3. D. 2.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


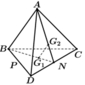
Gọi N là trung điểm của CD
● Khi đó A, G 2 , N thẳng hàng và B, G 1 , N thẳng hàng.
Do đó, B G 1 , A G 2 và CD đồng quy
![]() Áp dụng định lí Talet đảo, suy ra
Áp dụng định lí Talet đảo, suy ra
![]()
![]()
Do đó D sai. Chọn D.

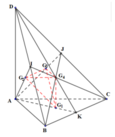
Gọi I, J, K lần lượt là trung điểm của BD, CD, BC.
Thể tích khối tứ diện vuông ABCD là:
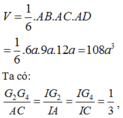
tương tự:
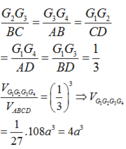
Chọn: A

Đáp án C.
Phương pháp
So sánh diện tích đáy và chiều cao của các khối chóp.
Cách giải
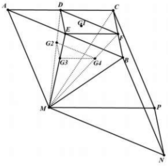
Gọi D, E, F lần lượt là trung điểm của AC, AB, BC.
Vì G 2 ; G 3 ; G 4 là trọng tâm các tam giác MAC, MAB, MBC nên
G 2 ∈ M D ; M G 2 = 2 D G 2 G 3 ∈ M E ; M G 3 = 2 E G 3 G 4 ∈ M F ; M G 4 = 2 F G 4 ⇒ G 2 G 3 G 4 / / D E F ⇒ V 1 = V E . G 2 G 3 G 4 = F G 3 M G 3 . V M . G 2 G 3 G 4 = 1 2 V M . G 2 G 3 G 4
Lại có
V M . G 2 G 3 G 4 V M D E F = M G 2 . M G 3 . M G 4 M D . M E . M F = 2 3 . 2 3 . 2 3 = 8 27
⇒ V 1 = 1 2 8 27 V M D E F = 4 27 V M D E F
Lại có
S D E F = 1 4 S A B C ⇒ V M . D E F = 1 4 V M . A B C = 1 4 . 1 3 V = 1 12 V
Vậy
V 1 = 4 27 . V 12 = V 81

1/ \(\overrightarrow{AM}=3\overrightarrow{AM}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}\)
\(\Leftrightarrow2\overrightarrow{AM}+3\overrightarrow{MG}=\overrightarrow{0}\)
\(\Leftrightarrow2\overrightarrow{AM}+3\overrightarrow{MA}+3\overrightarrow{AG}=\overrightarrow{0}\)
\(\Leftrightarrow\overrightarrow{AM}=3\overrightarrow{AG}\)
Ban tu ket luan
2/ Bạn coi lại đề bài, đẳng thức kia có vấn đề. 2k-1IB??
\(\overrightarrow{IA}+2k-1+\overrightarrow{IB}+k\overrightarrow{IC}+\overrightarrow{ID}=0\)



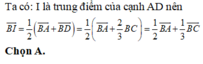
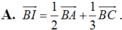
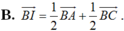
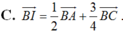
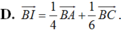

Khẳng định thứ (III) kia chính xác là gì nhỉ? Chắc chắn 30G là ko hợp lý rồi
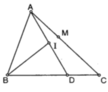
3D G