Ba lớp 7a, 7b, 7c được giao nhiệm vụ trồng 150 cây để phủ xanh đồi trọc. Tính số cây mỗi lớp. Biết 7a, 7b tỉ lệ với 5 và 3, 7b và 7c tỉ lệ với 2 và 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
Gọi số cây 3 lớp 7A, 7B, 7C trồng được lần lượt là x, y, z (x,y,z > 0)
Vì tổng số cây trồng của 3 lớp là 120 cây nên x+y+z = 120
Vì số cây trồng được của ba lớp 7A, 7B, 7C tỉ lệ với 7;8;9 nên \(\dfrac{x}{7} = \dfrac{y}{8} = \dfrac{z}{9}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\begin{array}{l}\dfrac{x}{7} = \dfrac{y}{8} = \dfrac{z}{9} = \dfrac{{x + y + z}}{{7 + 8 + 9}} = \dfrac{{120}}{{24}} = 5\\ \Rightarrow x = 5.7 = 35\\y = 5.8 = 40\\z = 5.9 = 45\end{array}\)
Vậy số cây 3 lớp 7A, 7B, 7C trồng được lần lượt là 35; 40; 45 cây.
7 tháng 5 2023
Gọi số cây mà `3` lớp trồng được lần lượt là `x,y,z (x,y,z \in \text {N*})`
Vì số cây của `3` lớp lần lượt tỉ lệ với `3:4:5`
Nghĩa là: `x/3=y/4=z/5`
Số cây trồng được của lớp `7A, 7B` nhiều hơn lớp `7C` là `40` cây
`-> x+y-z=40`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/3=y/4=z/5=(x+y-z)/(3+4-5)=40/2=20`
`-> x/3=y/4=z/5=20`
`-> x=20*3=60, y=20*4=80, z=20*5=100`
Vậy, số cây của `3` lớp lần lượt là `60` cây, `80` cây, `100` cây.
N
7 tháng 5 2023
Gọi số cây trồng được của 3 lớp 7A,7B,7C lần lượt là \(x,y,z\)(cây) \((x,y,z \in N*)\)
Do số cây trồng được của 3 lớp 7A,7B,7C lần lượt tỉ lệ với 3,4,5 nên:\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}\)
Do số cây trồng được của 2 lớp 7A,7B nhiều hơn số cây trồng được của lớp 7C là 40 cây nên \(x+y-z=40\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{3}=\dfrac{y}{4}=\dfrac{z}{5}=\dfrac{x+y-z}{3+4-5}=\dfrac{40}{2}=20\)
Do đó:
\(\dfrac{x}{30}=20\Rightarrow x=60\)
\(\dfrac{y}{4}=20\Rightarrow y=80\) \(\left(TM\right)\)
\(\dfrac{z}{5}=20\Rightarrow z=100\)
29 tháng 7 2023
Gọi số cây được trồng ở lớp $7A;7B;7C$ là $x,y,z$
Vì $y=20:21:y:z=7:9=21:27$, ta có:
$\dfrac{x}{20}=\dfrac{y}{21}=\dfrac{z}{27}=\dfrac{x+z+y}{20+21+27}=\dfrac{408}{68}=6$
Ta được: $x=6.20=120:y=6.21=126:z=6.27=162$
Lớp $7A$: $120:3=40$(cây)
Lớp $7B$: $126:3=42$(cây)
Lớp $7C$: 162:3=54$(cây)
LC
14 tháng 8 2015
Gọi số cây của 4 lớp lần lượt là a,b,c,d.
Theo bài ra ta có: a+b+c+d=172
a/b=3/4=>a/3=b/4=>a/75=b/100
b/c=5/6=>b/5=c/6=>b/100=c/120
c/d=8/9=>c/8=d/9=>c/120=d/135
=>a/75=b/100=c/120=d/135
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
a/75=b/100=c/120=d/135=a+b+c+d/75+100+120+135=172/430=2/5
=>a=2/5.75=30
=>b=2/5.100=40
=>c=2/5.120=48
=>d=2/5.135=54
Vậy lớp 6a trồng được 30 cây, lớp 6b trồng được 40 cây, lớp 6c trồng được 48 cây, lớp 6d trồng được 54 cây
HN
19 tháng 12 2017
7a c'ứ ko fải 6a
7b c'ứ ko fải 6b
7c c'ứ ko fải 6c
7d c'ứ ko fải 6d
30 tháng 10 2021
Gọi số cây trồng được của lớp 7A,7B,7C là a,b,c(cây)(a,b,c∈N*)
Áp dụng t/c dtsbn:
\(\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{3}=\dfrac{a+c-b}{4+3-6}=\dfrac{12}{1}=12\)
\(\Rightarrow\left\{{}\begin{matrix}a=12.4=48\\b=12.6=72\\c=12.3=36\end{matrix}\right.\)
Vậy....
30 tháng 10 2021
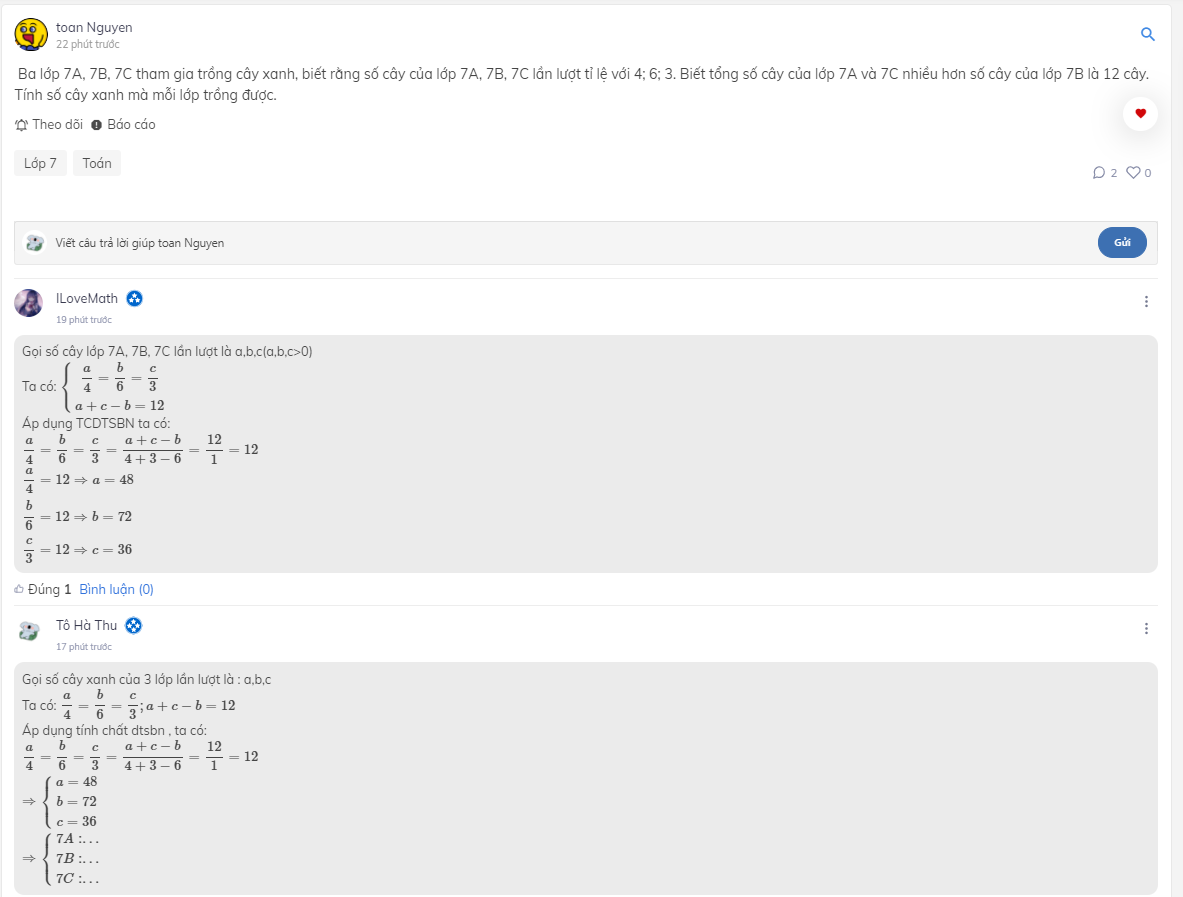
Gọi số cây lớp 7A, 7B, 7C lần lượt là a,b,c(a,b,c>0)
Ta có: \(\left\{{}\begin{matrix}\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{3}\\a+c-b=12\end{matrix}\right.\)
Áp dụng TCDTSBN ta có:
\(\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{3}=\dfrac{a+c-b}{4+3-6}=\dfrac{12}{1}=12\)
\(\dfrac{a}{4}=12\Rightarrow a=48\\ \dfrac{b}{6}=12\Rightarrow b=72\\ \dfrac{c}{3}=12\Rightarrow c=36\)
TH
30 tháng 10 2021
Gọi số cây xanh của 3 lớp lần lượt là : a,b,c
Ta có: \(\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{3};a+c-b=12\)
Áp dụng tính chất dtsbn , ta có:
\(\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{3}=\dfrac{a+c-b}{4+3-6}=\dfrac{12}{1}=12\)
\(\Rightarrow\left\{{}\begin{matrix}a=48\\b=72\\c=36\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}7A:...\\7B:...\\7C:...\end{matrix}\right.\)
30 tháng 10 2021
Gọi số cây lớp 7A,7B,7C ll là a,b,c(cây;a,b,c>0)
Áp dụng t.c dtsbn:
\(\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{3}=\dfrac{a-b+c}{4-6+3}=\dfrac{12}{1}=12\\ \Leftrightarrow\left\{{}\begin{matrix}a=48\\b=72\\c=36\end{matrix}\right.\)
Vậy ..
Lời giải:
Gọi số cây mà 3 lớp trồng được lần lượt là $a,b,c$ (cây)
Theo bài ra ta có: $a+b+c=150$
$\frac{a}{5}=\frac{b}{3}; \frac{b}{2}=\frac{c}{3}$
$\Rightarrow \frac{a}{10}=\frac{b}{6}=\frac{c}{9}$
Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{a}{10}=\frac{b}{6}=\frac{c}{9}=\frac{a+b+c}{10+6+9}=\frac{150}{25}=6$
$\Rightarrow a=10.6=60; b=6.6=36; c=6.9=54$ (cây)