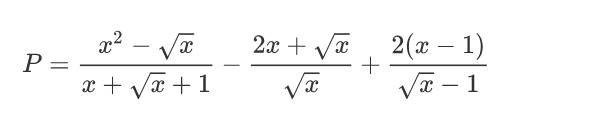
b, tìm x để biểu thức Q=2 căn x/P nhận giá trị là số nguyên
giúp em với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để (2x+2)/(x+3) là số nguyên thì \(x+3\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(x\in\left\{-2;-4;-1;-5;1;-7\right\}\)
\(\dfrac{2x+2}{x+3}=\dfrac{2\left(x+3\right)-4}{x+3}=2-\dfrac{4}{x+3}\in Z\\ \Leftrightarrow x+3\inƯ\left(4\right)=\left\{-4;-2;-1;1;2;4\right\}\\ \Leftrightarrow x\in\left\{-7;-5;-4;-2;-1;1\right\}\)

a: \(B=\dfrac{-x^2-4x-4-4x^2+x^2-4x+4}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{x-2}{2x-1}\)
\(=\dfrac{-4x^2-8x}{\left(x+2\right)}\cdot\dfrac{1}{2x-1}=\dfrac{-4x\left(x+2\right)}{\left(x+2\right)\left(2x-1\right)}=\dfrac{-4x}{2x-1}\)
b: |x|=3
=>x=3 hoặc x=-3
Khi x=3 thì \(B=\dfrac{-4\cdot3}{2\cdot3-1}=\dfrac{-12}{5}\)
Khi x=-3 thì \(B=\dfrac{-4\cdot\left(-3\right)}{2\cdot\left(-3\right)-1}=\dfrac{12}{-7}=\dfrac{-12}{7}\)

\(M=\dfrac{\sqrt{x}+5}{\sqrt{x}-2}=\dfrac{\sqrt{x}-2+7}{\sqrt{x}-2}=1+\dfrac{7}{\sqrt{x}-2}\)
Để M nguyên \(\Leftrightarrow\text{ }7\text{ }⋮\text{ }\left(\sqrt{x}-2\right)\)
=> \(\sqrt{x}-2\inƯ\left(7\right)=\left\{-7;-1;1;7\right\}\)
\(\Rightarrow\sqrt{x}\in\left\{1;3;9\right\}\)
\(\Rightarrow x\in\left\{1;9;81\right\}\)

a) x khác 2
b) với x<2
c) \(A=\frac{x\left(x-2\right)+2\left(x-2\right)+7}{x-2}=x+2+\frac{7}{x-2}\)
x-2=(-7,-1,1,7)
x=(-5,1,3,9)
a) đk kiện xác định là mẫu khác 0
=> x-2 khác o=> x khác 2
b)
tử số luôn dương mọi x
vậy để A âm thì mẫu số phải (-)
=> x-2<0=> x<2
c)thêm bớt sao cho tử là các số hạng chia hết cho mẫu
cụ thể
x^2-2x+2x-4+4+3
ghép
x(x-2)+2(x-2)+7
như vậy chỉ còn mỗi số 7 không chia hết cho x-2
vậy x-2 là ước của 7=(+-1,+-7) ok

a) \(A=\dfrac{\sqrt{x}+2}{\sqrt{x}-2}=1+\dfrac{4}{\sqrt{x}-2}\)
Để A nguyên thì 4 ⋮ √x - 2
\(\Rightarrow\sqrt{x}-2\inƯ\left(4\right)\)
\(\Rightarrow\sqrt{x}-2\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Rightarrow\sqrt{x}\in\left\{3;1;4;0;6;-2\right\}\)
Mà x \(\sqrt{x}\ge0\)
=> x thuộc {9; 1; 16; 0; 36}
b)

A∈Z⇒\(\dfrac{2\left(x+1\right)}{x+3}\in Z\Rightarrow\left(2x+2\right)⋮\left(x+3\right)\)
\(\Rightarrow\left(2x+6-4\right)⋮\left(x+3\right)\\ \Rightarrow\left[2\left(x+3\right)-4\right]⋮\left(x+3\right)\)
\(\text{Mà}2\left(x+3\right)⋮\left(x+3\right)\\ \Rightarrow-4⋮\left(x+3\right)\\ \Rightarrow x+3\inƯ\left(-4\right)=\left\{-4;-2;-1;1;2;4\right\}\\ \Rightarrow x\in\left\{-7;-5;-4;-2;-1;1\right\}\)
ĐKXĐ: \(x\ne\left\{0;1\right\}\)
Rút gọn được \(P=x-\sqrt{x}+1\)
\(\Rightarrow Q=\dfrac{2\sqrt{x}}{x-\sqrt{x}+1}\)
Do \(\left\{{}\begin{matrix}2\sqrt{x}\ge0\\x-\sqrt{x}+1=\left(\sqrt{x}-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\end{matrix}\right.\) \(\Rightarrow Q\ge0\)
\(Q=\dfrac{2\sqrt{x}}{x-\sqrt{x}+1}=\dfrac{2\left(x-\sqrt{x}+1\right)-2x+4\sqrt{x}-2}{x-\sqrt{x}+1}=2-\dfrac{2\left(\sqrt{x}-1\right)^2}{x-\sqrt{x}+1}\le2\)
\(\Rightarrow0\le Q\le2\)
Mà \(Q\in Z\Rightarrow Q=\left\{0;1;2\right\}\)
\(\Rightarrow\left[{}\begin{matrix}\dfrac{2\sqrt{x}}{x-\sqrt{x}+1}=0\\\dfrac{2\sqrt{x}}{x-\sqrt{x}+1}=1\\\dfrac{2\sqrt{x}}{x-\sqrt{x}+1}=2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}2\sqrt{x}=0\\x-3\sqrt{x}+1=0\\x-2\sqrt{x}+1=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x}=0\\\sqrt{x}=\dfrac{3+\sqrt{5}}{2}\\\sqrt{x}=\dfrac{3-\sqrt{5}}{2}\\\sqrt{x}=1\end{matrix}\right.\) \(\Rightarrow x=\left\{0;\dfrac{7+3\sqrt{5}}{2};\dfrac{7-3\sqrt{5}}{2};1\right\}\)