Cho tam giác ABC vuông tại à có AB = 9 cm BC = 15 cm AC = 12 cm
A) So sánh các góc, các cạnh của tam giác ABC
B) Trên tia đối của tia ab lấy điểm D sao cho A là trung điểm của đoạn thẳng BD Chứng minh tam giác ABC bằng tam giác ABC Từ đó suy ra tam giác BCD cân
C) EA là trung điểm cạnh CD be cắt AC ở I . Chứng minh đi qua trung điểm cạnh BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: AC=căn 15^2-9^2=12cm
AB<AC<BC
=>góc C<góc B<góc A
b: Xét ΔCBD có
CA vừa là đường cao, vừa là trung tuyến
=>ΔCBD cân tại C
c: Xét ΔCDB có
CA,DK là trung tuyến
CA cắt DK tại M
=>M là trọng tâm
=>CM=2/3CA=8cm

`@` `\text {dnv4510}`
`a,`
Xét `\Delta ABC:`
`\text {BC > AC > AB (5 cm > 4 cm > 3 cm)}`
`@` Theo định lý quan hệ giữa góc và cạnh đối diện
`=>` $\widehat {A} > \widehat {B} > \widehat {C}$.
`b,`
Ta có: A là trung điểm của BD
`-> \text {AC là đường trung tuyến}` `(1)`
K là trung điểm của BC
`-> \text {DK là đường trung tuyến}` `(2)`
Mà \(\text{AC }\cap\text{ DK = M}\) `(3)`
Từ `(1), (2)` và `(3)`
`-> \text {M là trọng tâm của} \Delta ABC`
`@` Theo tính chất của trọng tâm trong `\Delta`
\(\text{MC = }\dfrac{2}{3}\text{AC}\)
Mà \(\text{AC = 4 cm}\)
`->`\(\text{MC = }\dfrac{2}{3}\cdot4=\dfrac{8}{3}\left(\text{cm}\right)\)
Vậy, độ dài của MC là `8/3 cm`
`b,`
Ta có: \(\left\{{}\begin{matrix}\text{A là trung điểm của BC}\\\text{AC }\bot\text{ BD}\end{matrix}\right.\)
`->`\(\text{CA là đường trung trực}\)
Ta có: \(\left\{{}\begin{matrix}\text{AC là đường trung trực (hạ từ đỉnh A)}\\\text{AC là đường trung tuyến (hạ từ đỉnh A) }\end{matrix}\right.\)
`@` Theo tính chất của các đường trong `\Delta` với `\Delta` cân
`->` \(\Delta\text{ BDC cân tại C (đpcm).}\)
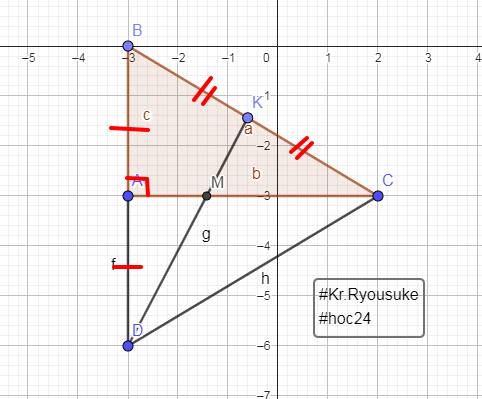
a: AB<AC<BC
=>góc C<góc B<góc A
b: Xét ΔCBD có
CA,DK là trung tuyến
CA cắt DK tại M
=>M là trọng tâm
=>CM=2/3CA=8/3cm
c: Xét ΔCBD co
CA vừa là đường cao, vừa là trung tuyến
=>ΔCBD cân tại C

a, Ta có : ∆ ABC vuông tại A ( gt)
-> BC^2 = AB^2 + AC^2 ( đ/lí Pytago )
-> AC^2 = BC^2 - AB^2
Mà BC = 10 cm ( gt ) ; AB= 6 cm ( gt)
Nên AC^2 = 10^2 - 6^2
-> AC^2 = 100- 36
-> AC^2 = 64
-> AC = 8 cm



Em tham khảo nhé.
A) Vì tam giác ABC vuông tại A nên góc A bằng 90 độ. Cạnh huyền là BC có độ dài 15 cm, cạnh đối là AC có độ dài 12 cm và cạnh kề là AB có độ dài 9 cm.
B) Gọi E là điểm đối của A trên tia BD. Ta cần chứng minh tam giác ABC bằng tam giác ABD để suy ra tam giác BCD cân.
Ta có:
- Vì A là trung điểm của BD nên AD = AB = 9 cm.
- Góc ABD = 90 độ (do AB vuông góc với BD).
- Góc ADB = góc ACB (cùng nằm trên cùng một cung AD của đường tròn ngoại tiếp tam giác ABC).
- Do đó, tam giác ABD đồng dạng với tam giác ACB.
Từ đó, ta suy ra tam giác ABC bằng tam giác ABD.
Vì AB = AD nên AE là đường trung bình của tam giác BCD. Do đó, ta có EI song song với BD (do A là trung điểm của BD).
C) Gọi M là trung điểm của BC. Ta cần chứng minh rằng E, I, M thẳng hàng để suy ra E là trung điểm của CD.
Ta có:
- Vì tam giác BCD cân nên trung trực của cạnh BC cũng là trung trực của cạnh BD. Do đó, M nằm trên trung trực của BD.
- Vì A là trung điểm của BD nên AM cũng là đường trung trực của BD.
- Từ đó, ta suy ra M nằm trên đường thẳng AE.
Ta cũng có EI song song với BD. Suy ra EI cũng nằm trên đường thẳng AM và kết hợp với điều trên, ta suy ra E, I, M thẳng hàng.
Do đó, ta chứng minh được rằng E là trung điểm của CD.
7uu