tìm nghiệm của : \(4x^3\)+9x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4x3-9x=0
x(4x2-9)=0
Vậy x=0 hoặc 4x2-9=0
Xét 4x2-9=0
4x2=9
x2=9/4
x=3/2 hoặc x=-3/2
Vậy đa thức có 3 nghiệm là x1=0, x2=3/2 và x3=-3/2


4x3+6x2+9x+7=0
<=>4x3+2x2+7x+4x2+2x+7=0
<=>x(4x2+2x+7)+(4x2+2x+7)=0
<=>(x+1)(4x2+2x+7)=0
\(\Leftrightarrow\left[\begin{array}{nghiempt}x+1=0\\4x^2+2x+7=0\left(2\right)\end{array}\right.\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x=-1\left(tm\right)\\\left(2\right)\Leftrightarrow4\left(x+\frac{1}{4}\right)^2+\frac{27}{4}>0\end{array}\right.\)
<=>(2) vô nghiệm
Vậy đa thức có 1 nghiệm duy nhất là x=-1

Khi P(x) + Q(x) ta đc
\(\left(9x-4x^3+3x^4-6x^2+1\right)+\left(4x^3-9x+5x^2-3x^4+1\right)\)
\(9x-4x^3+3x^4-6x^2+1+4x^3-9x+5x^2-3x^4+1\)
\(x^2+2\)
Ta có : \(C\left(x\right)=x^2+2=0\)
\(x^2=-2\)(vô lí)


c. Ta có h(x) = 0 ⇒ 5x + 1 = 0 ⇒ x = -1/5
Vậy nghiệm của đa thức h(x) là x = -1/5 (1 điểm)

G(x) = (x-3).(16-4x)
Nếu G(x) = 0 thì (x-3).(16-4x) => (x-3)= (16-4x)=0
* x-3 = 0 => x = 0 +3 =3 : 16 -4x =0 => 4x = 16- 0 => x = 16 : 4= 4
Vậy nó có hai nghiệm là 3 và 4
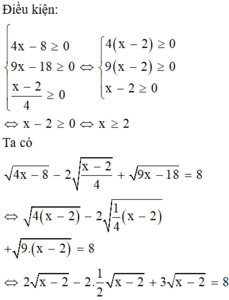
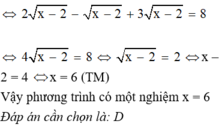
Ta có : \(4x^3+9x=x\left(4x^2+9\right)\)
Do \(4x^2+9>0\)
nên để \(4x^3+9x\) có nghiệm thì \(\Leftrightarrow x=0\)
`4x^3 +9x=0`
`<=>x(4x^2+9)=0`
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\4x^2+9=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x\in\varnothing\end{matrix}\right.\)