Cho tam giác AEC đồng dạng với tam giác ABD như hình vẽ, tính BD:
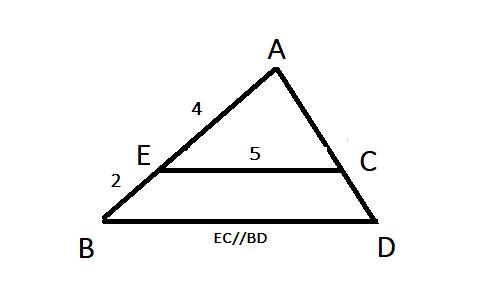
BD bằng:
A. 10 cm
B. 2 cm
C. 4 cm
D. 2,5 cm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 4 2022
\(AB^2+AC^2=3^2+4^2=25\)
\(BC^2=5^2=25\Rightarrow AB^2+AC^2=BC^2\)
\(\Rightarrow\Delta ABC\) vuông tại A với BC là cạnh huyền
\(\Rightarrow\) Bán kính đường tròn ngoại tiếp tam giác ABC bằng 1 nửa BC
\(R=\dfrac{5}{2}=2,5\left(cm\right)\)
4 tháng 11 2023
Xét ΔABC có \(\dfrac{AC}{sinB}=2R\)
=>\(2R=\dfrac{6}{sin150}=12\)
=>R=6(cm)
=>Chọn C
S
31 tháng 12 2021
Cho tam giác đều ABC độ dài cạnh là 6cm. Kẻ AI vuông góc với BC. Độ dài cạnh AI là:
A. 3√3 cm
B. 3 cm
C. 3√2 cm
D. 6√3 cm
19 tháng 9 2023
Theo bất đẳng thức tam giác:
a) Vì 2 + 3 = 5 nên bộ ba đoạn thẳng có độ dài 2 cm, 3 cm, 5 cm không thể là độ dài ba cạnh của một tam giác
b) Vì 3+4 > 6 nên bộ ba đoạn thẳng có độ dài 3 cm, 4 cm, 6 cm có thể là độ dài ba cạnh của một tam giác
* Cách vẽ: + Vẽ độ dài cạnh AB = 6cm.
+ Dùng compa, vẽ cung tròn tâm A bán kính 3 cm, cung tròn tâm B bán kính 4cm. Hai cung tròn này cắt nhau tại C.
Ta được tam giác ABC cần vẽ.
c) Vì 2+4 > 5 nên bộ ba đoạn thẳng có độ dài 2 cm, 4 cm, 5 cm có thể là độ dài ba cạnh của một tam giác
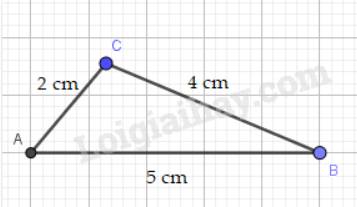
* Cách vẽ: + Vẽ độ dài cạnh AB = 5cm.
+ Dùng compa, vẽ cung tròn tâm A bán kính 2 cm, cung tròn tâm B bán kính 4cm. Hai cung tròn này cắt nhau tại C.
Ta được tam giác ABC cần vẽ.
HM
3
A.10cm
Do \(\Delta ACE\sim\Delta ABD\) nên ta có:
\(\dfrac{AE}{EB}=\dfrac{EC}{BD}\) hay \(\dfrac{4}{6}=\dfrac{5}{BD}\)
\(\Rightarrow BD=\dfrac{2.5}{4}=2,5cm\)
Vậy BD có độ dài là 2,5cm ⇒ Chọn D