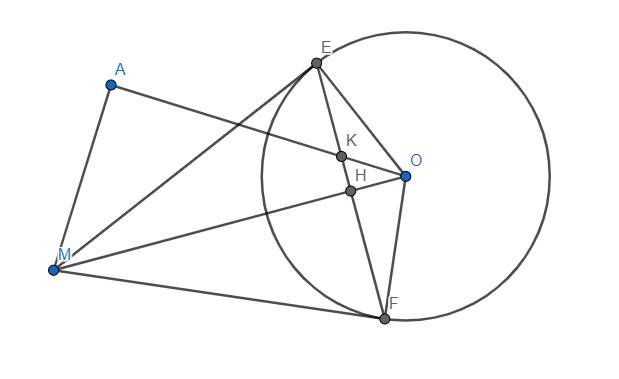
Cần hỗ trợ Cho điểm M nằm ngoài đường tròn (O

NB

Ngô bá đạo

22 tháng 3 2023 - olm

Cần hỗ trợ Cho điểm M nằm ngoài đường tròn (O; R). Vẽ tiếp tuyến MA ( A là tiếp điểm), cát tuyến MBC ( B nằm giữa M và C) và O nằm trong góc AMC. Vẽ OK vuông góc BC tại K . a) CM : tứ giác MAOK nội tiếp đường tròn. Xác định tâm và bán kính đường tròn này. b) vẽ dây cung AI // BC . CM góc IAK + góc AMO = 90 độ. c) IK cắt (o) tại điểm thứ hai là D. CM MD là tiếp tuyến...

Đọc tiếp

#Toán lớp 9

0

HN

Hường Nguyễn

5 tháng 12 2021

Cho đường tròn tâm O, điểm M nằm bên ngoài đường tròn, kẻ các tiếp tuyến MB, MA (A,B là các tiếp điểm)

a) Chứng minh OM là đường trung tuyến của tam giác MAB

b) Tính độ dài các cạnh của tam giác MAB, biết AO= 3

Mong các cao nhân trợ giúp :>>>

#Toán lớp 9

0

TT

thùy trâm

28 tháng 12 2021

Cho đường tròn (O; R) và điểm M bất kì, biết rằng OM = R . Chọn khẳng định đúng?
A. Điểm M nằm ngoài đường tròn (O; R)
B. Điểm M nằm trên đường tròn (O; R)
C.Điểm M nằm trong đường tròn (O; R)
D. Điểm M không thuộc đường tròn (O; R)

#Toán lớp 9

2

NL

Nguyễn Lê Phước Thịnh

28 tháng 12 2021

Chọn B

Đúng(2)

D

demonzero

28 tháng 12 2021

b

Đúng(1)

I

illumina

8 tháng 9 2023

(ko cần vẽ hình, giải chi tiết)Cho đường tròn (O; R) và điểm A nằm ngoài đường tròn. Vẽ đường thẳng d vuông góc với OA tại A. Trên đường thẳng d lấy điểm M khác điểm A. Qua điểm M vẽ hai tiếp tuyến ME và MF tới đường tròn (O) (E và F là các tiếp điểm). EF cắt OM và OA lần lượt tại H và K.1) Chứng minh: H là trung điểm của EF.2) Chứng minh rằng bốn điểm O, M, A, F cùng thuộc một đường tròn.3)...

Đọc tiếp

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

8 tháng 9 2023

1: Xét (O) cso

ME,MF là tiếp tuyến

=>ME=MF

mà OE=OF

nên OM là trung trực của EF

=>OM vuông góc EF tại H và H là trung điểm của EF

2: Xét tứ giác OFAM có

góc OFM=góc OAM=90 độ

=>OFAM nội tiếp

3: Xét ΔOFK và ΔOAF có

góc OFK=góc OAF

góc FOK chung

Do đó: ΔOFK đồng dạng với ΔOAF

=>OF/OA=OK/OF

=>OK*OA=R^2

Đúng(1)

TD

Trần Dương Minh Lộc

29 tháng 5 2022

Cho đường tròn (O) và điểm M nằm ngoài đường tròn. Từ M vẽ 2 tiếp tuyến MA, MB (A,B là tiếp điểm). Đường thẳng qua M cắt đường tròn (O) tại C, D (MC<MD) sao cho điểm O nằm trong tam giác BCD. Vẽ đường kính CE của đường tròn (O). Gọi S là giao điểm của EA và BCa) Cm tứ giác MAOB nội tiếp và OM vuông góc ABb) Cm tam giác OAM đồng dạng CASc) Cm tam giác OAC và MAS đồng dạng và tam giác MAS când) Gọi N là giao điểm...

Đọc tiếp

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

12 tháng 6 2023

a: góc MAO+góc MBO=180 độ

=>MAOB nội tiếp

Xét (O) có

MA,MB là tiếp tuyến

=>MA=MB

mà OA=OB

nên OM là trung trực của AB

=>OM vuông góc AB

b: góc CAE=1/2*180=90 độ

Xét ΔOAM vuông tại A và ΔCAS vuông tại A có

góc AOM=góc ACS

=>ΔOAM đồng dạng với ΔCAS

Đúng(0)

T

Tholauyeu

14 tháng 1 2023

Cho điểm O nằm ngoài đường thẳng a, cách a một khoảng 3cm. Vẽ đường tròn (O;5cm). Trên đường a lấy điểm A nằm ngoài đường tròn (O). Vẽ tiếp tuyến AM với đường tròn (O), ( M là tiếp điểm). Vẽ dây MN vuông góc với OA. Chứng minh khi A di chuyển trên a thì đường thẳng MN luôn đi qua một điểm cố định

#Toán lớp 9

0